Click here for a Microsoft word version of this essay.
In essay two the problem of tangent circles was explored. From that investigation the following conclusions developed:
1) when the center distance is greater than the sum of the lengths of the radii, circle T is externally tangent to the given circles;
2) when the center distance is equal to the sum of the lengths of the radii, circle T is congruent to one of the given circles, and, in fact, is the same circle;
and
3) when the center distance is less than the sum of the radii, circle T is internally tangent to one of the given circles and externally tangent to the other.
Circle T, just to refresh your memory, is the blue tangent circle for the given red circles. As we progress through essay three, we will retain the same relationship in color usage -- red for the given circles, and blue for the tangent circles.
Apolonius was a Greek mathematician who did some very interesting work in geometry. One problem he posed was as follows: Given three circles, construct a circle which is tangent to all three circles. After looking again at the definition of a hyperbola --the set of all points such that for any point in the set the difference of its distances from two fixed points is constant, the conclusions from essay two came to mind. The center of the tangent circle traces a hyperbola. In this essay we will attempt to locate these tangent circles for different configurations of three given circles.
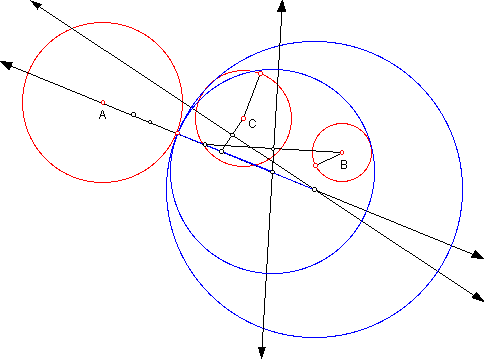
The logical question then arises: How can we extend the construction for tangent circles, studied in the previous essay, from two given circles to the case of three given circles? This is shown in Figure 1.

This is accomplished fairly easily: adding the third circle and constructing the circle tangent to the first circle, called circle A, and the third circle, called circle C, using, of course, the method for tangent circles in essay two.
Now, the challenge! Can we find the circle, actually a set of circles, which are tangent to the three red circles, regardless of the configuration? The algorithm used to accomplish this is as follows:
while animating the three red circles about the green circle (path of animation), trace the centers of the blue tangent circles. The trace of these centers is a hyperbola; where the two hyperbolas intersect is the center of the circle tangent to all three circles.
This investigation will look at the animation of circle A, circle B, and circle C,
for a standard size and position of the green circle, our path of animation. The standard position and size used for the first two figures is commonly known as the unit circle, where the center is located at the origin with a radius of one inch. Figure 2 shows the first circle tangent to the three red circles A, B, and C.
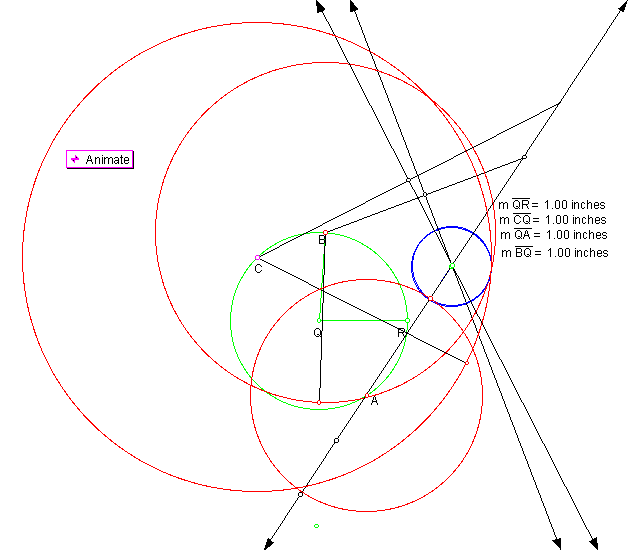
Notice this circle occurs when circle B is internally tangent to circle C and overlaps circle A.
In Figure 3 we see yet another configuration.
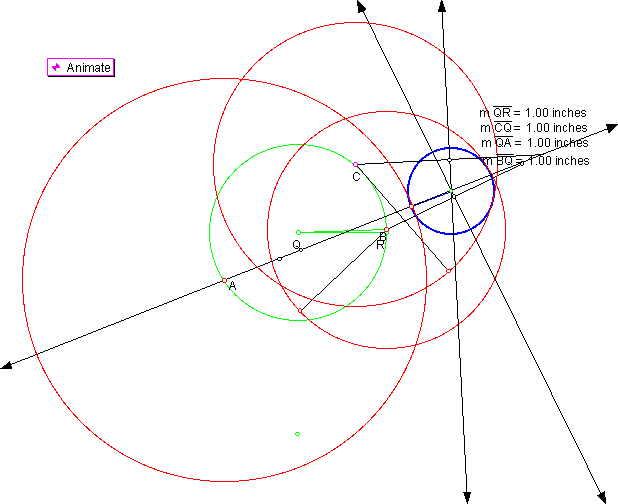
Here the three circles overlap each other with none of the given circles internally or externallly tangent to each other.
In the next two figures, the circle has been moved on the unseen grid (hidden to better see the intersection points on the hyperbolas) to x = 1. In Figure 4 you see the first of these circles.

In Figure 4 we see both circles B and C internally tangent to the blue tangent circle while circle A is externally tangent to it. There is no overlap whatsoever in circles A, B, or C.
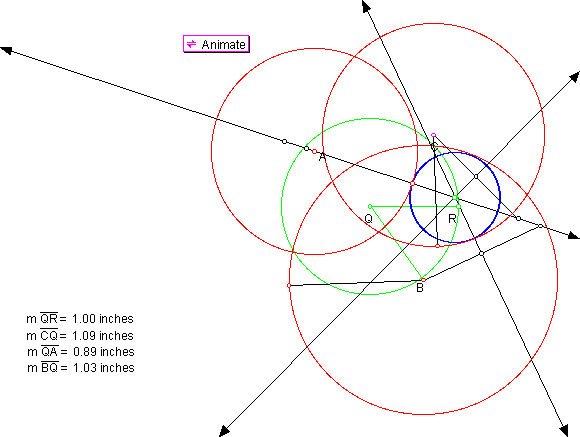
In Figure 5 we see circles A, B, and C overlapping; the blue tangent circle is internally tangent to two of the red ones, C and B, while externally tangent to A. You may notice that the distance to the centers of the circles is not exactly 1.00 as it should be. This happens because the animation oftentimes goes past the desired point and some manipulation on the Sketchpad is necessary to get the figure back to the tangency points.
For the next set of two figures, the position of the center of the green circle has moved to y = 1 on the unseen axes. Figure 6 is the first of these figures.

Figure 6 shows that the blue tangent circle is internally tangent to circles B and C, while externally tangent to circle A. Again the red circles are overlapping.
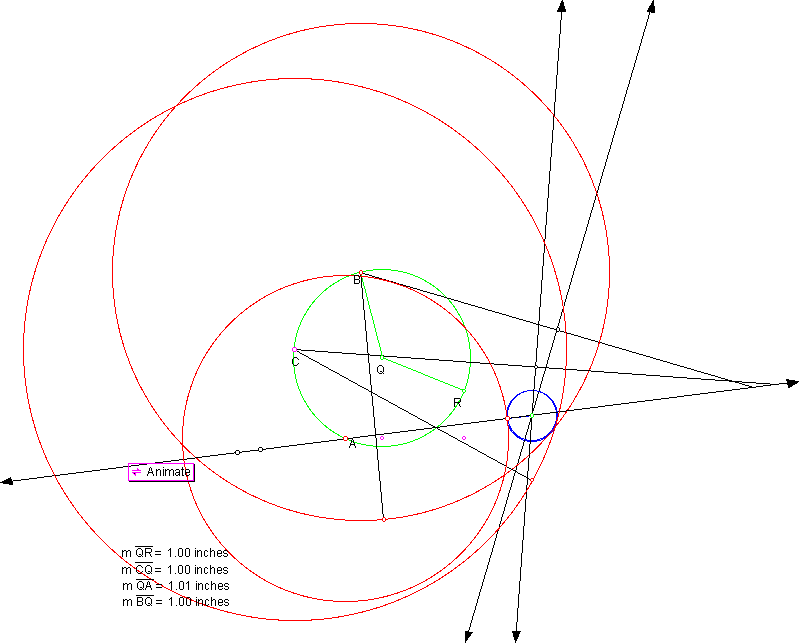
Here we have a different configuration on the three red circles: circle A is in the interior of circle C with two pairs of the circles overlapping each other. The resulting blue tangent circle is very small; however, it is still internally tangent to circles B and C and externally tangent to A.
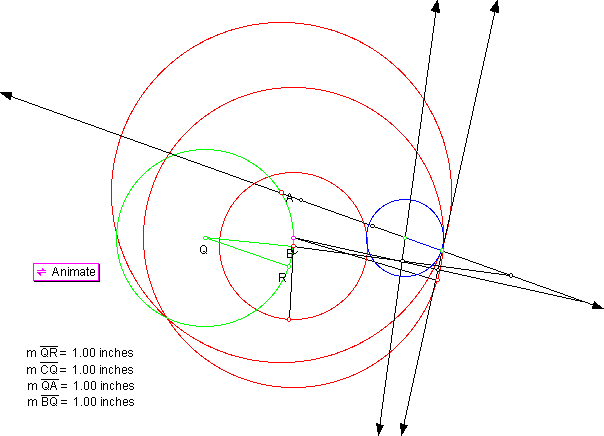
In Figure 8 we see the configuration which has circles B and C concentric, a totally new arrangement, but the blue tangent circle is still externally tangent to one circle while internally tangent to the other two. This has the green circle located at x = - 1; this position seems to give us only one circle which is tangent to all three red ones.
Now, we will locate the green circle at y = - 1 and look at the configurations which give us the blue tangent circles.
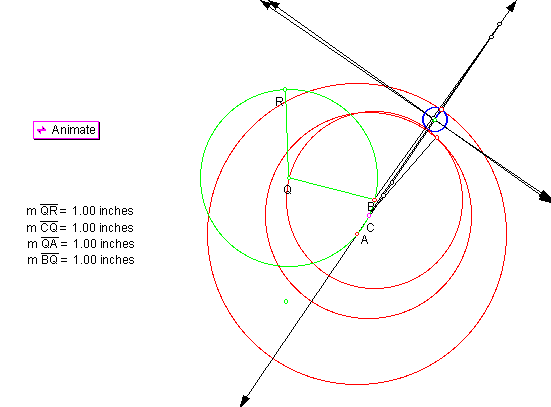
In this configuration the blue tangent circle is externally tangent to two of the red circles and internally tangent to the third. Notice this is reversed to what we have seen in previous positions.
When the circles are overlapping, we see the blue tangent circle externally tangent to one red circle and internally tangent to the other two. If the circles do not overlap, the blue tangent circle is externally tangent to all three red circles. Apolonius found eight different tangent circles for a set of three given circles. We have explored and found all but one of these, that being the blue tangent circle which sits externally tangent to the three red circles with each red circle external to the blue one.
Back to Teresa Banker's Home Page