This unit is designed for students who have successfully completed the first year of algebra. It is assumed they have a working knowledge of geometry for this unit. Application and understanding of the figures and concepts employed with circles such as point, line, segment, angle, coplanar, etc. would come under this assumption. Figures, demonstrations, and some proposed problems are implemented with the use of The Geometer's Sketchpad. Exercises for the first lesson have been laid out in detail; subsequent lessons may or may not be this detailed.
Objectives
1. Define a circle and terms related to it.
2. Apply theorems that relate tangents and radii.
3. Apply theorems about the chords of a circle.
Student behavioral objectives: the student will be able to
1) draw and label parts of a circle given certain conditions;
2) draw conclusions given parts of a circle and conditions based on them;
3) tell whether points are interior, exterior, or on the circle; and,
4) tell the number of intersection points with the circle determined by the given figure
and its location in relation to the circle.
Lesson 1 : Basic Terms
A circle is the set of points in a plane that are a given distance, called the radius, from a given point in the plane, called the center. A segment from the center to a point on the circle is called a radius. All radii of a circle are congruent. For a demonstration of these definitions click here.
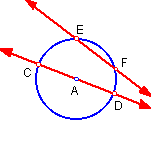
A chord is a segment that joins two points on a circle. A diameter is a chord that passes through the center. A secant is a line that contains a chord.

In the figure, segment EF is a chord; segment CD is a diameter; segment AD is a radius, with point A the center; line EF is a secant.
Congruent circles are circles that have congruent radii. By definition, radii of congurent circles are congruent. What do the circles in the figure have in common? If you said the center point A, you are correct. These are concentric circles.
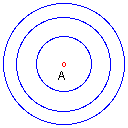
Can you think of other natural phenomena which suggest concentric circles?
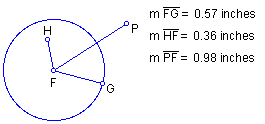
definition: In a plane, the interior of a circle is the set of points whose distance from the center is less than the radius. The exterior of a circle is the set of points in the plane whose distance from the center is greater than the radius.
In the figure, segment FG is the radius; since FP > FG, point P is in the exterior of the circle; since FH < FG, point H is in the interior of the circle.
EXERCISES
In exercises 1 - 6, draw and label the following in circle P.
1. A radius, segment PX 2. A secant, line YQ 3. A diameter, segment YZ 4. A segment PA, such that PA > PX 5. A segment PB, such that PB < PX 6. A segment PR, such that PB < PR < PA
7. Draw a circle and several parallel chords. What do you think is true of the midpoints of
all such chords?
8. Point Z lies on circle X. How many chords can you draw that contain Z? How many
diameters? How many radii?
Circle R contains point A. Tell whether B is an interior point, an exterior point, or on the circle.
9. R(4, 1) ; A(3, 7) ; B(2, -7) 10. R(2, 4) ; A(9, 3) ; B(6, -1)
11. R(8, 11) ; A(12, 7) ; B(4, 7) 12. R(-3, 3) ; A(0, -4) ; B(5, 2)
13. Points A and B are on circle P. Is segment AB a diameter if P(5, 5), A(8, 9) and B(2, 1) ?
14. Point W lies on outside circle O and point X lies inside. In how many points does the
figure named intersect the circle?
a. segment WX b. ray WX
c. ray XW d. segment OX
**Some problems were taken from Scott, Foresman and Company Geometry (page 326), while others came from Houghton Mifflin Geometry (pages 294 - 295 ).
Student behavioral objectives: the student will be able to
1) apply theorems and/or definitions relating to tangents of circles and tangent circles.
Lesson 2 : Tangents
Definition: A tangent to a circle is a line in the plane of the circle that intersects the circle in exactly one point. The point of intersection is called the point of tangency.
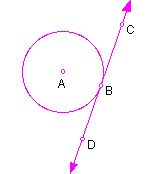
In the figure, line DC is a tangent; point B is the point of tangency. A ray or segment is tangent if it is a part of a tangent line and contains the point of tangency. So, ray BC is a tangent ray and segment BC is a tangent segment.
Theorem: If a line is tangent to a circle, then the line is perpendicular to the radius drawn to
the point of tangency.
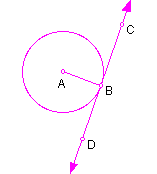
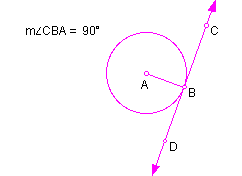
In the figure on the left, angle CBA appears to be a right angle. On the right, after taking the measure of angle CBA, we see it is a 90 degree angle, the definition of a right angle; therefore, line CD is perpendicular to the radius AB.
Theorem: In the plane of a circle, if a line is perpendicular to a radius at a point on the circle, then the line is tangent to the circle.
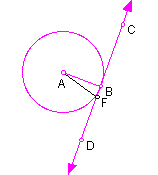
In the figure, we would choose point F as any point on line CD. To show line CD is perpendicular means AF > AB by the fact that the perpendicular segment from a point to a line is the shortest segment from the point to the line, that is, segment AB. To see a demonstration that this remains true except when point F is the same as point B <click here.> demtan.gsp
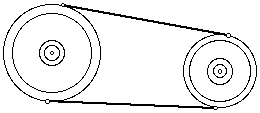
This sketch of a fanbelt in a motor system suggests a tangent relationship for two circles.
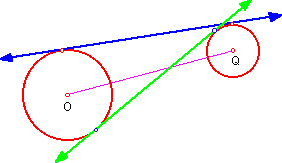
In the figure, segment OQ joins the centers of the two red circles.
Definiton: A common tangent is a line that is tangent to each of two coplanar circles.
Common external tangents do not intersect the segment joining the centers of
the circles. The blue line is a common external tangent to the two circles.
Common internal tangents do intersect the segment joining the centers of the circles. The green line is a common internal tangent.
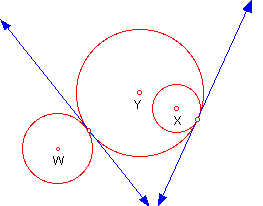
Definition: Tangent circles are two coplanar circles that are tangent to the same line at the same point.
Circles W and Y are externally tangent circles while circles Y and X are internally tangent circles.
Three or more circles are mutually tangent if each pair of them are tangent.
EXERCISES
Part 1. Using two circles for each sketch, illustrate several configurations which satisfy conditions for common internal/external tangents. (about 5 examples)
Part 2. Use the diagram to find lengths of different segments based on tangent line AC, diameter AB, secant BQ (intersecting line AC at C).
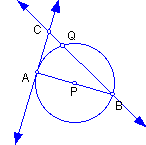
Sample problem: If BC = 13 and AC = 5, find AB. (about 5 examples)
Part 3. Using the same diagram in Part 2, use the converse of the Pythagorean Theorem to find the indicated length so that line AC is a tangent. Lines AC and BQ are in the plane of circle P with diameter AB.
Sample problem: If PB = 4 and AC = 6, then BC = ?. (about 5 examples)
Part 4. Problems with internal and external tangents. (about 5 examples)
**Problems suggested from Scott, Foresman and Company Geometry (page 329 - 330).
Part 5. 1 - 3 Make sketches to show all possible positions of three (2. four 3. five) mutually tangent circles.
4. Write a conjecture about the number of possible positions for n mutually tangent circles if n is a whole number greater than four.
**Problems taken from Merrill Geometry Enrichment Worksheet (page 55).
Student behavioral objectives: the student will be able to
1) solve locus problems involving tangents using construction methods related to tangents.
Lesson 3: Construction Exercises
Constructions for these exercises may be done in two ways:
1) the conventional use of compass and straight edge; or
2) the software package The Geometer's Sketchpad.
1. Construct a line tangent to a circle at a given point on the circle.
(You might begin by using the construction of a perpendicular through a given point.)
2. Given a point outside a circle, construct two tangents to the circle from the given point.
3. After completing the construction of #2, use construction methods to show that the tangent segments are congurent.
4. Extention from #2. Construct the circle tangent to the sides of angle ABC as shown in the figure below.
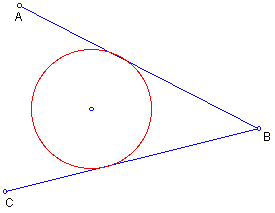
In the figure, the red circle is tangent to angle ABC. If you would like to try this construction,
<click here>. angtan.gsp
Student behavioral objectives: the student will be able to
1) state and apply theorems relating to chords of the circle.
Lesson 4: Chords of a Circle
Definition: A chord is a segment whose endpoints lie on a circle.
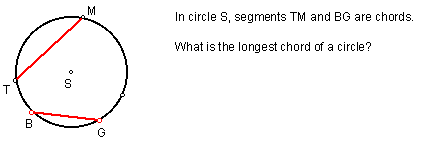
Theorem: If a line through the center of a circle is perpendicular to a chord, it bisects the chord.

Theorem: In the same circle or in congruent circles, if two chord are the same distance from the center, then the chords are congruent.

Theorem: In the same circle or in congruent circles, if two chords are congruent, then they are the same distance from the center.
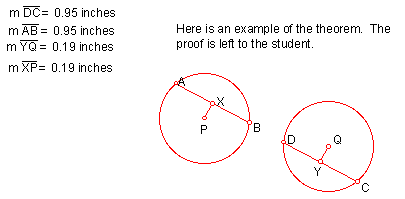
EXERCISES
Part 1. Use the diagram to find different lengths in the circle. AC is a diameter of circle P, PD is perpendicular to AB, and AB is a chord.

Part 2. Using the figure, find lengths of chords and distances from the center. (about 5 )

Part 3. Mary Ellen has only part of a circular piece of pattern for her quilt. She must determine the diameter of the circle in order to get enough fabric. Describe how she could determine the diameter.
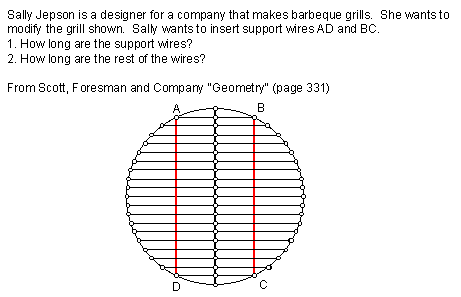
Part 4. Given the grill from before, find the length of the support bars AD and BC if the grill top is 22 inches in diameter and the support wires are 6 inches apart.
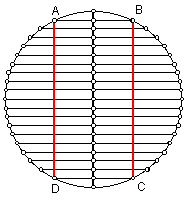
**Some problems were taken from Scott, Foresman and Company Geometry (page 333), while others came from Houghton Mifflin Geometry (page 325 ).
Possible additions to this unit would include those theorems and definitions which relate the measures of chords and their arcs, secant and tangent segments, and intersecting chords of the circle.