Versions of the problem are relative common in problem collections
in contexts such as hanging art for exhibit in museums (modern
museum exhibits often display work on a sloping surface). The
"perpendicular" case also sees expression in the position
along the side of a soccer field to have the best angle for a
shot or the inane discussions of football sportscasters to argue
for taking a 5-yard penalty to kick a field goal "from a
better angle" now that the rules have been changed to narrow
the width of the goal posts.
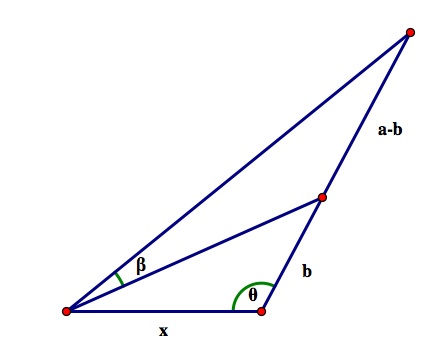
Some Labels:
As the left end of the segment of length x
moves along the line at eye level, that point and points at the
top and at the bottom of the billboard define a circle with inscribed
angle q across the segment of length a - b. The maximum angle
will occur when the circle is tangent to the line at eye level,
that is, when the circle has only one point in common with the
line at eye level.
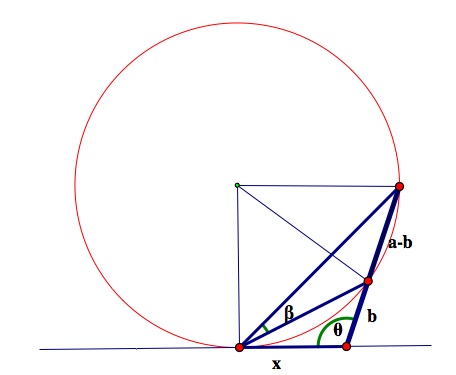
Any other point on the line at eye level will
have a smaller inscribed angle.
From elementary geometry, the square of the tangent segment from
a point is equal to the product of the secant segment and the
external portion of the secant segment. That is,
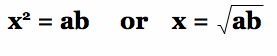
Since the segments of length a and b
are given in the problem by the positions of the line and
the billboard, and since x is the geometric mean of a
and b, the circle tangent to the line and through the points
at the top and bottom of the billboard can be constructed.
Note: This result and the solution holds for either
direction the billboard is tilted, or before the wind blew:
Wind from the West
Before the Wind
Wind
from East
Return to problem statement.