

Hint
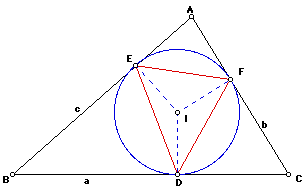
Look at quadrilateral AEIF. The angles at E and F are right angles since EI = FI = DI -- radii of length r of the inscribed circle. Therefore angles EAF and EIF are SUPPLEMENTARY. That means that
sin(EAF) = sin(EIF) More simply they equal sin A
Now consider the triangle EIF. Two of its sides are of lenght r and the included angle has sine equal to sin A.. The area is
In a similar manner we can write the areas of triangles EI D and DIF. So the area of the Pedal triangle in the inscribed circle is
End of hint!!. Now the problem is to express sin A + sin B + sin C in terms of a, b, and c.