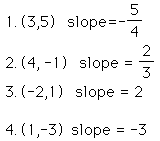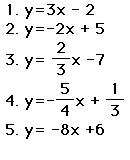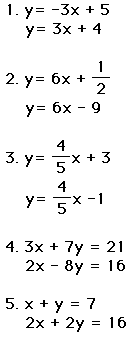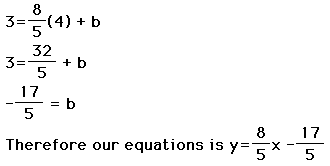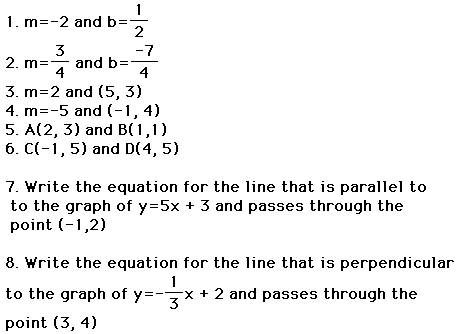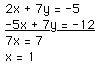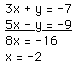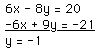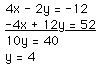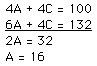Goals
1. The students will be able to effectively compute the slope of lines.
They will use this knowledge to compare the slopes of parallel and perpendicular
lines.
2. The students will be able to write lines in slope intercept form and
point slope form.
3. The students will be able to solve systems of equations using ordered
pairs, graphing and substitution.
4. The students will be able to solve systems of equations by adding, subtracting
and multiplying.
Day 1: Slope of a line
Slope of a segment is the ratio of the "rise" or the vertical
distance over the "run" or the horizontal distance.
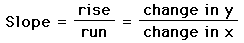
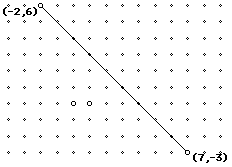
Now, given 2 points connected by a segment on a graph, count the slope
using the above definition.
Example #1
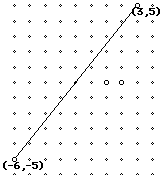
Example #2
Some rules for finding slope:
1. Always find the change in y first and let that be your numerator,
then find the change in x and let that be your denominator.
2. When counting UP, that is a positive number.
When counting DOWN, that is a negative number.
More Examples
Plot the following points, connect them and count the slope using the
rules that you know
1. (4,3) (-1, 1)
2. (-3, -7) (2,4)
3. (0,2) (3,5)
4. (5,0) (-1, 4)
Now, pick your own sets of 2 points. Use graph paper to plot these points
and connect the dots. Compute the slope for each line that you have drawn.
Do 5 examples this way using the graph paper given.
Day 2 : Slope (con't)
Let's review the definition of slope:
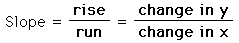
Compute the slope of the following lines.
Example #1
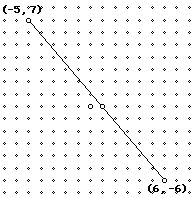
Example #2
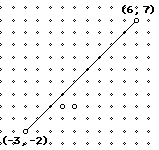
What happens to the slope of lines that are vertical and horizontal?
Compute the slopes and put the calculations into the calculator and see
what you get.
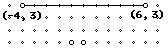
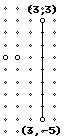
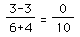
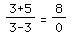 We call this "0 slope" We call this "No slope"
(Notice, here we cannot
divide by 0!)
We call this "0 slope" We call this "No slope"
(Notice, here we cannot
divide by 0!)
What can we call lines with a positive slope?
These lines go up or "increase"
What can we call lines with a negative slope?
These lines go down or "decrease"
An easier way to write the slope formula is:
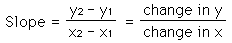
Now, graph the line that passes through the given point and has the given
slope.
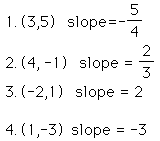
Day 3: Parallel and Perpendicular Lines
Explore the following:
1. Plot the following points
A(-10, 0) B(6, 12) C(-4, -5) D(12, 7)
Next, draw the segments AB and CD. What do you notice?
Find the slopes of each line segment.
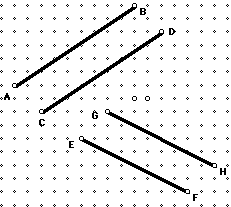
2. Investigate the following diagram:
What pairs of segments appear to be parallel?
Find the slope of each segment. What is true?
3. Based on the results in 1 and 2, what conclusion can you make about
the slope of parallel lines?
4. Now plot the following points:
A(-1, 3) B(5, -6) C(6, 1) D(-3, -5)
Draw the segments AB and CD. What do you notice about these segments?
Find the slopes of these line segments. What is their relationship to each
other?
What do you get when you multiply these slopes together?
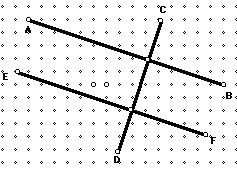
5. Investigate the following diagram:
What pairs of lines appear to be perpendicular?
Find the slope of each segment. What is true?
What do you get when you multiply these slopes together?
6. Based on the results 4 and 5, what conclusion can you make about
the slopes of perpendicular lines?
Conclusions
* If two lines are parallel, they have the same slope.
* If two lines are perpendicular, the have a slope that is the negative
reciprocal and their product is -1. Investigate the slopes above. Is
this true?
Use Geometer's Sketchpad to compute the slopes of the following points and
find the slope of a line parallel and the slope of a line perpendicular
to the given line.
1. A(6, 3) and B(4, 6)
2. C(-1, -5) and D(3, -2)
3. E(0, 5) and F(-1, 6)
4. G(-4, -2) and H(-5, -2)
Now, using Algebra Xpresser to find 3 lines parallel to each other and 2
lines perpendicular through the parallel lines. Give each slope and two
points that lie on each line.
Day 4: Slope-Intercept Form of an Equation
The standard form that equations are written in is called slope-intercept
form of the line where y=mx + b. In this form, m represents the slope
and b represents the y-intercept. The y-intercept is the point where
the graph crosses the y axis.
Find the slope and y-intercept of the following lines.
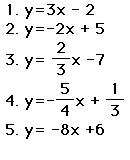
Now, using Algebra Xpresser, graph the above lines.
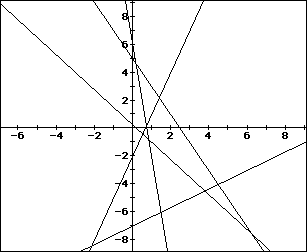
Determine whether the 2 lines are parallel, perpendicular or neither.
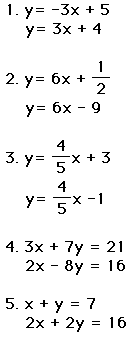
Now, plug these equations into your TI-82 calculator. Check to see of you
were correct about your assumptions of slope.
Day 5: Writing Equations for Lines
When writing an equation, you nust look at the information that is given
to you.
1. For example, write an equation for a line with slope=4 and y-intercept
that is 2.
Given: m=4 and b=2
Therefore, the equation in y=mx + b form is y=4x + 2.
Now, what is the slope and a point on the line were given?
2. Write an equation for a line whose slope is 5 and contains the point
(3, -2).
Given: m=5, x=3 and y=-2.
The form for the equation is y=mx + b and we are looking for the
y-intercept.
So, -2 = 5(3) +b
-2 = 15 +b
b= -17
Therefore, the equation for the line is y=5x - 17.
What happens if you are given 2 points?
3. Write the equation for the line that passes through the points
(4, 3) and (-1, -5).
Given two points, we can easily find the slope of this line.
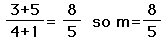
Now, we have slope also x=4 and y=3 (or we could have picked the other point
to use.)
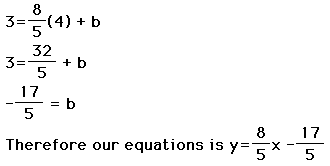
Using the information that we now know about writing the equation of lines
using the given slope, point, and/or y-intercept, try some on your own.
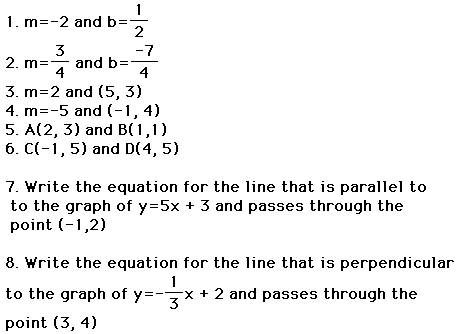
Day 6 and 7: Systems of Equations
An ordered pair is a solution of a systems of equations if it is
a solution for each of the equations.
State whether the ordered pair is a solution of the system of equations.
1. (2, -3)
2x - y = 10
x + 2y = -5
Solution:
2(2) - (-3) = 10
4 + 3 = 10
7 = 10
2+2(-2) = -5
2 - 4 = -5
-2 = -5.
So, (2, -3) is not a solution for this system of equations.
2. (2, 5)
-4x + y = -3
2x + y = 9
Solution:
-4(2) + 5 = -3
-8 + 5 = -3
-3 = -3
2(2) + 5 = 9
4 + 5 = 9
9 = 9.
So, (2, 5) is a solution for this system of equations.
To solve a system of equations using graphs, graph each equation on
the same pair of axes. All points of intersection are solutions to
the system of equations.
Solve each system of equations by graphing.
3.a. y = 2x - 6
b. y = x - 4
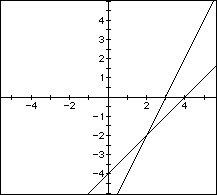
By looking at the graph of these two equations, you can clearly see
that they intersect at (2, -2). Once we find an intersection point, we must
put that value into both of our original equations to see if the point satifies
both equations.
Check your intersection point:
a. -2 = 2(2) - 6
-2 = 4 - 6
-2 = -2
b. -2 = 2 - 4
-2 = -2.
Now we can see that the point (2, -2) is a solution for the system of equations.
4.a. 3x-2y=4
b. 2x+y=5
In order to graph these equations, we need to put them in y=mx+b form.
So,
a. 3x - 2y = 4
-2y = -3x + 4
y = (3/2)x - 2
b. 2x + y = 5
y = -2x + 5.
Now, graph the two lines.
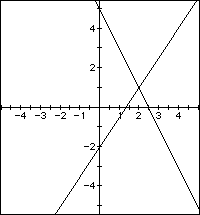
From the graph of these two equations, we can clearly see that (2, 1)
is the intersection point of the two lines. Now we must check our point
to see if it satisfies both equations.
Check your intersection point:
a. 3(2) - 2(1) = 4
6 - 2 = 4
4 = 4
b. 2(2) + 1 = 5
4 + 1 = 5
5 = 5.
So, the point (2, 1) is a solution to the system of equations.
More examples:
Solve the systems of equations by graphing:
1. y = 3x - 1
y = 3x + 2
2. y = -x + 7
y = 2x - 5
3. x + 3y = 6
3x + 2y = 4
4. y = 7 - 3x
6x + 2y = 14
5. y = 4x - 2
x - 4y = 2
Day 8: Substitution
One of the methods of solving systems of equations is called substitution.
This method is helpful when one of the equations is already solved for one
variable. For substitution, you need to eliminate one variable so that you
will have the equation in one variable to solve.
Steps for substitution:
1. Solve one of the equations for one variable in terms of the other.
2. Substitute that expression in the other equation and solve.
3. Substitute that value in one of the original equations and solve.
4. Check in both of the original equations.
Solve by the substitution method:
1. x + y = 6
x - 2y = 3
Step 1:
x + y = 6
y = -x + 6
Step 2:
x - 2(-x+6) = 3
x + 2x - 12 = 3
3x - 12 = 3
3x = 15
x = 5.
Step 3:
5 + y = 6
y = 1.
Step 4:
a. 5 + 1 = 6
6 = 6
b. 5 - 2(1) = 3
5 - 2 = 3
3 = 3.
So, the point (5, 1) is a solution for this system of equations.
2. 2x - y = 14
x + y = 7
Step 1:
x + y = 7
y = -x + 7.
Step 2:
2x - (-x + 7) = 14
2x + x - 7 = 14
3x - 7 = 14
3x = 21
x = 7.
Step 3:
7 + y = 7
y = 0.
Step 4:
a. 2(7) - 0 = 14
14 = 14
b. 7 + 0 = 7
7 = 7.
So, the point (7, 0) is a solution to this system of equations.
3. x - 2y = -9
-2x + 4y = -13
Step 1:
x - 2y = -9
x = 2y - 9.
Step 2:
-2(2y - 9) + 4y = -13
-4y + 18 +4y = -13
18 = -13 is not true.
So, there is no solution to this system of equations.
4. At the food truck, Joe bought 3 hot dogs and 4 drinks for $10. Cindy
paid $5 for 1 hot dog and 3 drinks. Find the cost of each hot dog and each
drink.
Let h=hot dog and d=drink
3h + 4d = 10
1h + 3d = 5
Step 1:
1h + 3d = 5
h = -3d + 5.
Step 2:
3(-3d + 5) + 4d = 10
-9d +15 + 4d = 10
-5d + 15 = 10
-5d = -5
d = 1.
Step 3:
h + 3(1) = 5
h + 3 = 5
h = 2.
Step 4:
a. 3(2) + 4(1) = 10
6 + 4 = 10
10 = 10
b. 1(2) + 3(1) = 5
2 + 3 = 5
5 = 5.
So, each hot dog cost $2 and each drink cost $1.
More examples:
Use substitution to solve the systems of equations:
1. -2x + y = 2
4x - 2y = 3
2. 2x + y = 3
-12x - 6y = -18
3. x + y = 5
2x - y = 4
4. -2x + y = -3
3x - 3y = -18
5. Jim bought 4 jars of jelly and 6 jars of peanut butter. Adam bought 3
jars of the same jelly and 5 jars of the same peanut butter. Jim paid $19.32
and Adam paid $15.67. What is the cost of a jar of peanut butter?
6. On a construction site there are 14 cranes and trucks. Three times the
number of cranes is 2 more than twice the number of trucks. How many cranes
are there on the site?
Day 9: Adding and Subracting to Solve Systems of Equations
Warm-Up Activity:
Simplify these expressions:
(3x - y -6)- (3x - 2y - 6) = y
(4x + y + 4) + (2x - y - 10) = 6x - 6
Steps to follow when adding or subtracting:
1. If the coefficients of one of the variables are opposites, add
the equations to eliminate one of the variables. If the coefficients of
one of the variables are the same, subtract the equations to eliminate
one of the variables.
2. Solve the resulting equation for the remaining variable.
3. Substitute the value for the variable in one of the original equations
and solve for the unknown variable.
4. Check the solution in both of the original equations.
Solve the systems of equations by adding or subtracting:
1. 2x + 7y = -5
-5x + 7y = -12
Steps 1 and 2:
subtract the two equations and solve for resulting variable
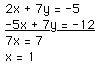
Step 3:
2(1) + 7y = -5
2 + 7y = -5
7y = =7
y = -1.
Step 4:
a. 2(1) + 7(-1) = -5
2 - 7 = -5
-5 = -5
b. -5(1) + 7(-1) = -12
-5 - 7 = -12
-12 = -12.
So, the point (1, -1) is the solution to the system of equations.
2. 3x + y = -7
5x - y = -9
Steps 1 and 2:
solve using addition and solve for resulting variable
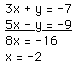
Step 3:
5(-2) - y = -9
- 10 - y = -9
-y = 1
y = -1
Step 4:
a. 3(-2) + (-1) = -7
-6 - 1 = -7
-7 = -7
b. 5(-2) - (-1) = -9
-10 + 1 = -9
-9 = -9.
So, the point (-2, -1) is a solution for the system of equations.
More Examples:
Solve by adding or subtracting:
1. x - y = -5
x + y = 15
2. 6x - 3y = 6
8y = -6x - 16
3. x - y = -1
x + y = 11
4. 5x + 4y = 12
4y = 3x - 4
5. x - y = -1
x + y = 9
Day 10: Multiplying to Solve Systems of Equations
Solve the systems of equations by multiplying:
1. 3x - 4y = 10
3y = 2x - 7
Step 1: In order to solve this system, we need to multiply each equation
by a constant so that one of the variables has a coefficient that is either
opposite or the same.
2(3x -4y = 10) = 6x -8y = 20
3( -2x +3y = -7) = -6x + 9y = -21
Step 2: Since the coefficients of x are opposites, we need to add
these two equations together.
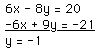
Step 3: Now, we must solve the resulting equation for the remaining
variable.
3x - 4(-1) = 10
3x + 4 = 10
3x = 6
x = 2.
Step 4: Again, we need to check the solution in both of the original
equations.
a. 3(2) - 4(-1) = 10
6 + 4 = 10
10 = 10
b. -2(2) +3(-1) = -7
-4 - 3 = -7
-7 = -7.
So, the point (2, -1) is a solution for this system of equations.
2. 4x = 2y - 12
3y = x + 13
Step 1:
4x - 2y = -12
4(-x + 3y = 13) = -4x + 12y = 52
Step 2:
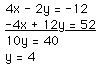
Step 3:
3(4) = x + 13
12 = x + 13
x = -1
Step 4:
a. 4(-1) = 2(4) -12
-4 = 8 -12
-4 = -4
b. 3(4) = -1 + 13
12 = -1 + 13
12 = 12.
So, the point (-1, 4) is a solution to this system of equations.
3. WORD PROBLEM:
Tim sold 25 movie tickets for a total of $132. If each adult ticket sold
for $6 and each children's ticket sold for $4, how many of each kind did
he sell?
Let A=Adult tickets and C=Child tickets
So, since Tim sold 25 Adult and Child tickets, we can set up this equation:
A + C = 25
Since, Tim sold Adult tickets for $6 and Child tickets for $4, we can set
up this equation:
6A + 4C = $132
Our system of equations is:
A + C = 25
6A + 4C = 132
Now, solve this system by multiplying the first equation by 4:
Step 1:
4(A + C = 25) = 4A + 4C = 100
Step 2:
By subtracting the two equations we get:
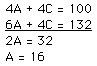
Step 3:
16 + C = 25
C = 9.
Step 4:
a. 16 + 9 = 25
25 = 25.
b. 6(16) + 4(9) = 132
96 + 36 = 132
132 = 132.
So, Adult tickets cost $16 and Child tickets cost $9.
More Examples:
Solve the systems of equations by multiplying:
1. x - 5y = 0
3y = 2x - 7
2. 5x + 3y = 12
4x - 5y = 17
3. y = 3x + 8
4x - 2y = -14
4. 7x + 4y = 4
2x + 3y = -10
5. Adult tickets for a benefit breakfast cost $2.50. Children's tickets
cost $1.50. If 56 tickets were sold for total sales of $97, how many of
each kind were sold?
6. A class of 31 students was divided into seven groups consisting of 4
or 5 students each. How many of each size group were there?
7. Jason spent $130 on six items of clothing consisting of jeans and shirts.
If jeans cost $27 each and shirts cost $19 each, how many of each did he
buy?
Return to Homepage
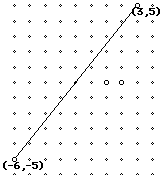


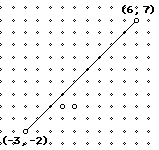

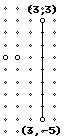
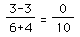
We call this "0 slope" We call this "No slope" (Notice, here we cannot divide by 0!)