
The Mathematics Education Department
EMT 725, Lisa F. Garey

![]()
Click here for the Problem statement
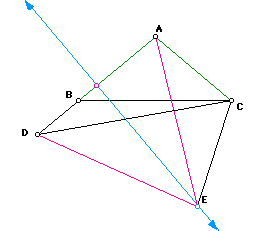
The problem asks for the measure of angle BCD. As the hint suggested, constructing a perpendicular line through the midpint of AD gives us AE = DE, where E is any point on that perpendicular line.
![]()
Let ADE be an equiateral triangle. 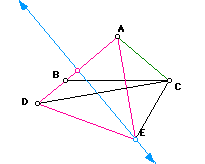
Then we have 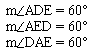 .
.
The hint also suggested reflecting along CD. When ADC and their segements are reflected along CD, the image is conruent with EDC. Then we have a kite where the opposite angles are equal.
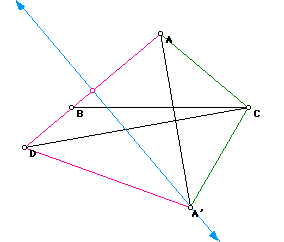
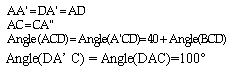
The interior angle sum of any quaddrilateral is 360. Let angle BCD be x. Hence,
360 = angle(DAC)+ angle(ADA') + angle(DA'C) + angle(A'CA)
= 100 + 60 + 100 + (40+x) + (40+x)
x = 10 degrees = angle(BCD)
Click here for an active GSP sketch.
![]()
Return to Lisa's EMT 725 Problems