W. Courtney Trabue
EMT-725 Problem Solving
Dr. Jim Wilson (Spring 1997)
Problem Statement: What is the volume of a 12 ounce can ?
Problem Approach:
Reading Labels and Volume Conversions for Cooking:
Volume can be expressed numerous ways. Using cooking measurements I could
say a can of 12 fluid ounces is equivalent to one and a half cups. I could
also buy a
can of Coke (12 fluid ounces) and simply read off the side of the can to
get the metric
measure in cubic centimeters ( 355 mL = 355 cu cm ). This is of course an
approximation of the actual volume because the conversion factors used by
industry to lable products always
rounds off.
Using Technology ( the Calculator )
Any advanced calculator will convert volume measurements in fluid ounces
to cubic
inches or cubic centimeters automatically. I used my TI-92 calculator to
get the equivalent measurement of 12 fluid ounces in terms of cubic centimeters
and cubic inches.
12 ounces = 354.88 cubic centimeters = 21.656 cubic inches
The Old Human Measurement (subject to BIG TIME ERROR)
I measured a standard Coke can in the chemistry lab at Georgia Military
College, Ft. Gordon
campus using a calliper and tape which resulted in the following:
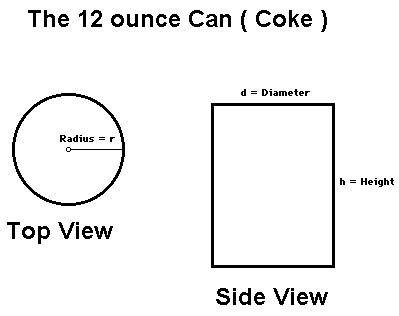
height = 4.75 inches
diameter = 2.6 inches
circumference = 8.1875 inches
By assuming the can is approximately a "Right Circular Cylinder",
I can use the formula I learned in high school algebra for estimating volume:
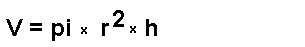
I estimated that the volume was about 25.219 cubic inches.This estimate
is "OFF". A Coke can is not "exactly" a Right Circular
Cylinder. The top and bottom are smaller than the average mid section of
the can. And, the contents of the can, the liquid Coke, does not fill the
can to the top. (Shaded area represents liquid)

I measued the Coke can from the top of the can to the bottom on the first
trial, and from bottom to top on the second trial. I took the average of
the two measurements as my hieght. Since the actual contents of the can
is somewhat lower than the measured height of the can, my volume estimate
is on the high side.
This estimate could be imporved were I to measure the actual height of the
liquid in the can several times and take the average. Unfortunately, I can
not see through the metal can, so the liquid height can only be estimated
by reducing the can height slightly.
I would still have the problem of using an approximate geometric solid (
the right circular cylinder) to represent the Coke can. The model does not
compensate for taper at the top and bottom.
Extensions:
1. Extimate the volumes and surface areas of different sizes of containers,
not just cylinder types.
2. Try to figure out the minimum and maximum surface areas for a given volume.
Return to Court's Home Page


