

Problem: Estimate the number of cubic yards of material in a waste stockpile that has the following measures and outline. The material has been accumulated by trucks and other equipment driving up onto the pile by a road that was formed up the side of the waste site. It is roughly oval in shape with ridges formed as in the outlines below.
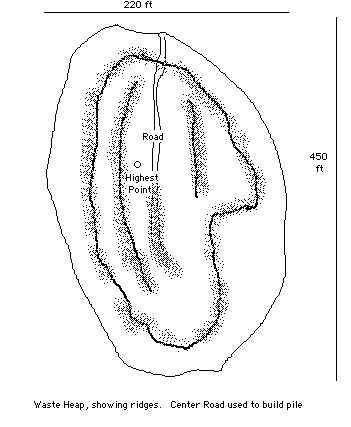
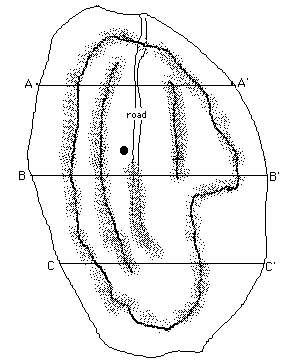
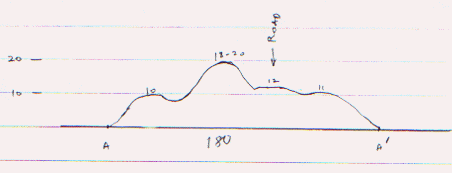
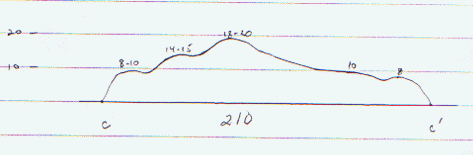
On the next drawing, three cross-sections of the pile have been drawn and the measures for critical points shown. This helps visualize the irregular shape of the pile as well as give some measurements that may prove useful in producing an estimate. Each cross-section is on a "graph" so by interpolation heights at any point along the cross section can be estimated.
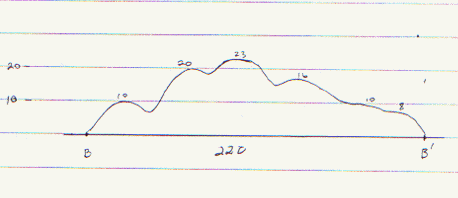
Making an estimate
Various approaches might be considered. One method is to estimate the area of a horizontal cross section and calculate a volume estimate for some segment of the pile by multiplying by a linear distance perpendicular to the cross-section. For example, suppose K, L, and M represent the areas of the cross-sections AA', BB', and CC' respectively. A section 75 feet on either side of each cross-section would then give an estimate of the volume for that sector of the pile as 150(K) + 150(L) + 150(M). We could get more precise estimates by taking more cross-sections.
Suggestion: See Area of Golf Greens or Area of Texas for strategies for estimating the area of irregular shapes.
Note: For using this strategy, the cross-sections would need to be drawn to scale.
The problem for estimating the volume of water in a flowing stream has, as a supporting problem, the need for estimating the area of a region bounded by a line and a curve. An analogous strategy will work here. For example if three heights are selecect and spread along the base, then the three areas are an estimate of the area between the base and the curve. We can do a better estimate by chosing more heights and spreading them evenly along the length of the base.
Suggestion: An estimate could be made from the arithmetic mean of the heights positioned evenly across a cross-section and multiply this by the base to get an average area. Then multiply this by the sector length to get an estimate for that part of the volume.
If the height of the cross section was a function f(x) for x ranging from A to A' along the x-axis, then the the integral of this range would give the area. We can approximate this numerically by taking n evenly spaced measures for f(x) across the range. For a gross estimate n does not need to be large.
In this example, take 8 evenly spaced heights across each cross-section. Multiply the arithmetic mean by the length of the base to get an estimate of the number of square feet in the cross-section. Now multiplty by 150 feet to get an estimate for the number of cubic feet in the sector of the pile for which the cross section is the center.For more precision we would take more cross sections or more heights within each cross section. Once you have an estimate for the number of cubic feet in the pile, divide by 27 to get the number of cubic yards.
Set up a hand calculator routine for doing these computations, or set up a spread sheet template.
What is the estimate you obtained?
Mark off 10 percent above and below your estimate to give a range. What is the range?
How confident are you that the actual volume is within the range you obtained?
Click here for a solution following this strategy.
A Different Strategy
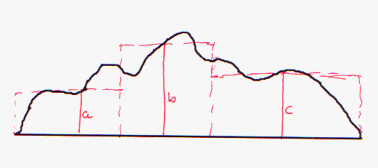
One way to segment the pile is to model it with a stack of half-elliptical disks stacked together. The representation in the cross-section is like this:
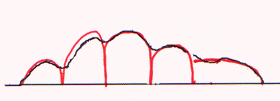
The cross-section of each piece is approximated by a half ellipse. The area of an ellipse with major semiaxis a and minor semiaxis b is approximately
. Then the volume of the half-elliptical disk can be approximated by
where t is the width of a segment of the pile. The approximate segmentation was guided by the following sort of outline. Area E had the shape of a quarter ellipse on its side. Additional measures were taken for the lengths and the heights were read from the cross-section charts.
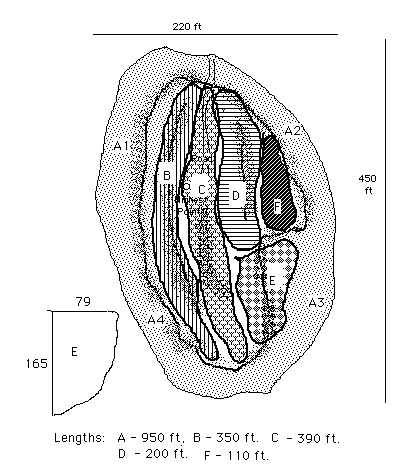
| AREA | VOLUME | Cubic yds | |
| A | |
(253)(950) cu. ft. | 8902 |
| B | |
(677)(350) cu. ft. | 8776 |
| C | |
(690)(390) cu. ft. | 9967 |
| D | |
(573)(200) cu. ft. | 4246 |
| E | |
(10238)(11.5) cu. ft. | 4361 |
| F | |
(501)(110) cu. ft. | 2041 |