---

---

---

Harmonic Mean Problems

---

Note: There are multiple related problems on this page. Consider all of them.

Given segment AB with parallel intersecting segments AE and BC on the same side of AB. Construct the segments AC and BE, intersecting at F and construct the segment FG parallel to AE and BC with G on AB.   (You may want to create your own GSP file to implement this construction.)

Prove:

---

Discussion:

Clearly, one approach is to use similar triangles.

   and   

Add the two equations together, substitute and symplify. . .

---

Interpret

Let FG = x, AE = a, and BC = b. Then

or

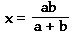
For positive a and b, x is ONE-HALF the harmonic mean of a and b.

Reference:

Charosh, M. (1965) Mathematical Challenges. Washington, DC: National Council of Teachers of Mathematics. Problem 30.

 

---

Other Problems using the Harmonic Mean

Isosceles trapezoid diagonal intersection

Average Rate

The Harmonic Mean

A Tangled Tale Problem

Inscribed Squares in a Triangle

 

---

Construction Problem

Given two line segments, find geometric constructions of a segment with length that is the harmonic mean of the lengths of the given two segments.   Implement with GSP.   One guide would be the introductory problem on this page.