PROBLEM SOLVING WITH HERON'S FORMULA
Heron's formula for the area of a triangle with sides of length a, b, c is
where
It is unfortunate that this topic has essentially disappeared
from school curriculum today. Calculation, given available calculations
and computers, can no longer be a reason for avoiding the formula.
In what follows, I hope to show some interesting and challenging
problems using Heron's formula.
Whether or not one would pose the demonstration or proof of Heron's
formula for a particular class would depend on the class. Initially,
exploration with Heron's formula could involve computing areas
using the formula and making comparison's of the results -- much
as we pose analogous exercises in a meaningful way with the Pythagorean
theorem long before a proof or demonstration is fully understood.
For instance, one exercise could be to have students measure the
sides and an altitude on several triangles and, with calculator,
compute the areas with both formulas
Comparison of the results could well lead to intuitions about
the areas of triangles and understanding of when one formula would
be more applicable than the other.
Consider this problem. What different triangular regions could be formed by 100 feet of fencing? What would be the area of each? What questions could you ask about the shapes or the areas?
The demonstration and proof of Heron's formula can be done from elementary consideration of geometry and algebra. I will assume the Pythagorean theorem and the area formula for a triangle
where b is the length of a base and h is the height to that base.
We have
so, for future reference,
There is at least one side of our triangle for which the altitude lies "inside" the triangle. For convenience make that the side of length c. It will not make any difference, just simpler.
Let p + q = c as indicated. Then
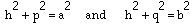
This demonstration of Heron's formula is straightforward and elementary.
Working through it with students can provide fruitful ideas of
strategy, symmetry, planning, and observation. We now switch to
consider some problems and investigations for which Heron's formula
is useful.
Show that the maximum area of a triangular region with a fixed
perimeter occurs for an equilateral triangle.
Comment. I would adapt the statement and context of this problem
depending on the background of the students. Above, I mentioned
an exploratory investigation where students looked at different
triangular regions that could be formed with a perimeter of 100
feet. Now extend this. Have students organize a table where the
lengths of the sides are varied systematically .
In order to vary something "systematically" one needs
to identify a variable that can be ordered in the table. For example,
investigate the more manageable problem of isosceles triangles.
Let the side of length a be the base to vary from 2 to
48 in steps of 2, as follows
Table a b c A _______________________________ 2 49 49 48.9897949 4 48 48 95.9166305 6 47 47 140.712473 8 46 46 183.303028 10 45 45 223.606798 12 44 44 261.533937 14 43 43 296.984848 16 42 42 329.84845 18 41 41 360 20 40 40 387.298335 22 39 39 411.582313 24 38 38 432.666153 26 37 37 450.33321 28 36 36 464.327471 30 35 35 474.341649 32 34 34 480 34 33 33 480.832611 36 32 32 476.235236 38 31 31 465.403051 40 30 30 447.213595 42 29 29 420 44 28 28 381.051178 46 27 27 325.269119 48 26 26 240
This table can be generated with a calculator in only a few minutes and the data open up lots of opportunity for discussion, plausible reasoning, and problem posing.
and equality occurs when s - a = s - b = s - c, that is, a = b
= c. Since the product is always less than this constant, this
constant is the maximum for the product and the maximum area of
a triangle with a fixed perimeter 2s is
The equilateral triangle has that maximum area. For instance,
the maximum area for all triangles having a perimeter of 100 is
Interpret the condition
What can be concluded for any triangle for which the condition holds?
