

Take a rectangular sheet of paper (1 below). Fold it in half to make a crease down the center of the sheet from top to bottom (2 below). Then, select a point on the crease and make another crease from the upper right corner to the point (3 below); now make a crease from the upper left corner to the point (4 below).
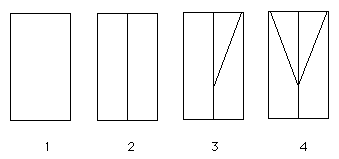
How would the point be selected so that the triangle formed by the top of the sheet and the two slant creases is the same area as each of the lateral trapezoids?
First, get some sheets of paper and do some folding to get a feel for the problem. We can make a fold across any two points and a point is certainly indicated where two creases cross or where a crease intersects an edge of the paper.
Folds can be used to bisect a line segment. Like, the bottom of the page is a line segment. We can fold corners of the page to form a crease that is the perpendicular bisector. Proof?
Second, folding to trisect a line segment (e.g. folding the paper into thirds) is probably a guessing game. If you claim it is a "folding" construction you should have a proof that the fold trisects the segment (exactly, not approximately).
Third, of course you will want to switch to a line drawing representation for analysis and proof at some point. Use similarity concepts to show an exact folding construction for the desired configuration.
Extension:
How is the problem changed if the first fold is horizontal at the middle of the page?