

Problem
Two spheres are placed in a corner of a room (e.g. beachball & orange). The spheres are each tangent to the walls and floor and and tangent to each other. Find the ratio of the radii of the larger sphere to the smaller.
Write-up

First, visualize a slice through the centers of the two spheres down the corner of the room and along the 45 degree angle in the floor.
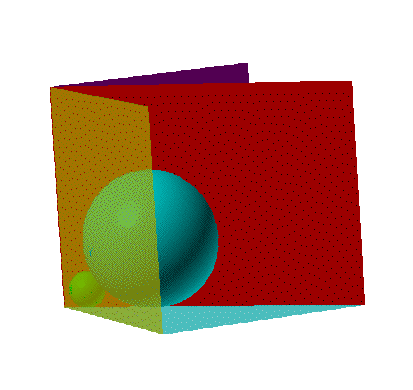
The slice, or cross-section, will have two circles tangent to one side (the line along the 45 degree angle) of a right angle and tangent to each other. The circles do not touch the vertical axis of the corner of the room.
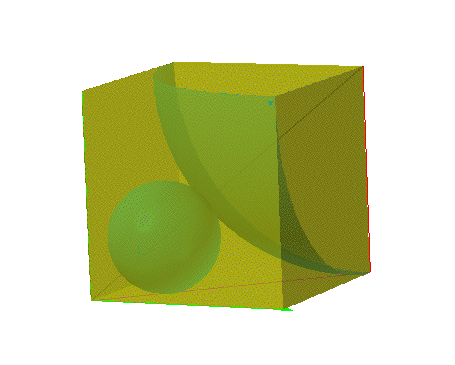
Let the radius of the large sphere (circle) be a and the radius of the small sphere (circle) be b as in the sketch below.
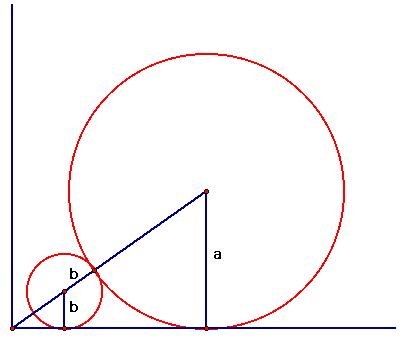
Now, look at the segment from the center of the large circle down through the center of the small circle and on to the corner of the room. I can express that length in two ways. First it is the diagonal of a cube with side of length a. Therefore the segment is of length
It is also of length because the distance from the center of the smaller circle can also be thought of as the diagonal of a smaller cube
So I can write an equation:
Divide each side of this equation by b.
Simplify:
Solve: