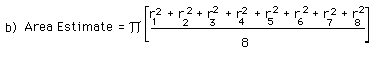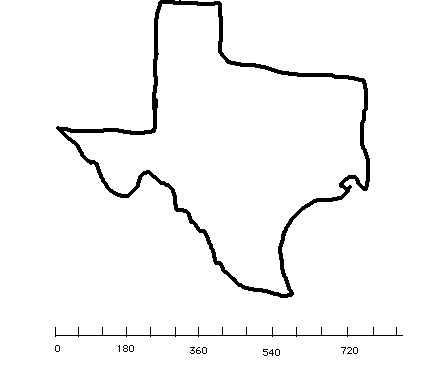
Problem: Estimate the area of Texas, in square miles, given the following map and the indicated scale. We will use the same map and scale in miles on the subsequent problems.
Discussion items:
How might we estimate the area of this irregular shape? If you have a proposal, write down the procedure and carry through to get an estimate.
Some examples that have come up.
A. Take a string and lay it along the outline. Then when completed, measure the string, divide by 4, and square the get an estimate of the area.
B. Move the string until it forms a circle and then find the area of that.
C. Find the smallest rectangle that includes all of the map, take the largest rectangle that fits entirely within the state and take the average of the areas.
D. Same as C, but with circles.
E. Cover the map with a grid and count the squares on the grid . . .
F. Same as E, but count those entirely within the map, count those on the border, and . . . like we did in grade school . . .
Each of these provides an opportunity (and a need) for clarifying some ideas about area and about estimates of area. Each provide an opportunity for questions such as
a. Why is his a reasonable estimate?
b. Would the procedure work for the map of another state? For example, would the perimeter stuff work as well for California?
c. How would you change your procedure to get a better estimate?
Suggestion F, of course has been a part of elementary school textbooks for years and different variations of it are intended to obtain an inner measure and an outer measure and estimate the area of the irregular shape by the arithmetic mean of the inner area and the outer area. More precision could come from using a finer grid. Each unit square is 60 miles on each side.
The strategy of inner and outer rectangles is illustrated by the following. It has the drawback of no obvious way to improve the estimate. In this case it is pretty clear that this procedure would produce an overextimate.
