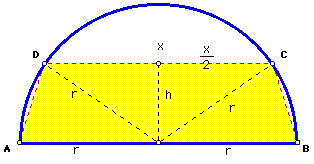
To use the Arithmetic Mean-Geometric Mean Inequality let's set up the equation for the area as follows. The goal is to use the AM-GM Inequality to show the are is always less than or equal to some constant value and thus reaches a maximum at that point.

=

=

The product of the four terms under the radical is the target for use of the AM-GM inequality. For that substitution to yield an expression with only constant terms (i.e. eliminate the x-variable), however, the coefficients of the x terms need to add to 0. This could be done if the first term had a coefficient of 3. So consider the following equivalent expression.

=

Now, by the AM-GM inequality, applied to the 4-term expression under the radical, we have

Area =

=

=

=

So the area is always less than or equal to this constant term, and by the AM-GM inequality, the equality is reached if and only if

That is,

x = r

Thus, the maximum area occurs when the shortest base of the trapezoid is the length of the radius of the semicircle, and that area is

Return