

Given a semicircle of radius r. What is the maximum area of any trapezoid inscribed in the semicircle?
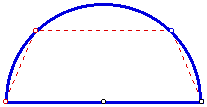
Click here to call a GSP animation to see the area of the inscribed trapezoid vary.
This picture assumes that the trapezoid of maximum area will have its longest base along the diameter of the semicircle. What about trapezoids oriented such as the following picture? What argument can be given to show they are never the maximum area?
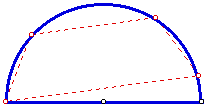
Click HERE to call a GSP animation to see the area of the inscribed trapezoid vary.
There is no loss of generality in considering the case of a semicircle with unit radius. The maximum area of any trapezoid inscribed in a semicircle of radius r will be
times the maximum area of a trapezoid inscribed in a semicircle of unit radius. (WHY?)
1. Use a Spreadsheet to estimate the maximum area. One approach is as follows. The longest base is of length 2r (on the diameter of the semicircle) and we can let Column A contain measures of the altitude h from 0 to r. Then the measure of the other base will be
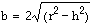
and these values can be put in Column B. Column C can accumulate the calculated area of the trapezoids. Click here to see an Excel Spreadsheet for r = 10 where the altitude is increased in steps of .25. The Series 2 graph represents the areas of the trapezoids.
At what height is the area a maximum? What is the length of the shorter base at that point?
2. Write a function for the area and use a graphing program to show the curve and to estimate the maximum area. Use a graphing calculator or a computer graphing program.
Hint (if needed).
3. Use the Arithmetic Mean-Geometric Mean Inequality to find the exact area and to prove it is the maximum.
Hint: Let x be the length of the shorter base.
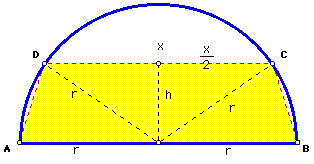
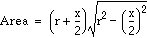
Help, if needed.
4. To avoid thinking about it, use calculus. Set up a function for the area and set the first derivative to zero to locate a relative maximum.
5. Use Geometry. Consider a reflection of the semicircle and inscribed trapezoid in the diameter of the semicircle. The trapezoid and its reflection combine into a hexagon inscribed in a circle . . .
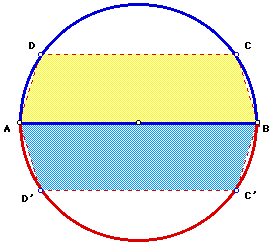
Is it known that of all hexagons inscribed in a circle, the maximum area will occure when the hexagon is regular? If so, this problem is solved. If not, how would one prove it?
Extension
Consider the perimeter of the trapezoid where the shorter base ranges from 2r to 0. Is there a maximum perimeter? If so, what is it? What is the length of the shortest base when the perimeter is at a maximum?
Let x be the length of the shortest base. See below. Similar triangles ACB and AKC will give an easily calculated length for a slant side s in terms of r and x.
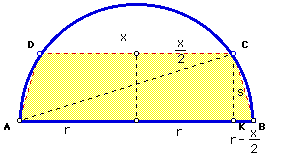
Perimeter help, if wanted.