

In these problems, information is given about a triangle to identify physical attributes. The problem is to describe ruler and compass constructions of the triangle from the given attributes. For consistent notation adapted to this environment I use the following:
The angles at vertices A, B, C: A, B, C
The sides of the triangle opposite vertices A, B, C: a, b, c.
The medians: ma, mb, mc
The altitudes: ha, hb, hc
The segments along an angle bisector to the opposite side: da, db, dc
The radius of the circumcircle: R
The radius of the incircle: r
The radii of the excircles: ra, rb, rcThe notation: b+c will mean "given a line segment equal in length to the sum of the lengths of sides b and c.
1. Triangle, given two sides and the median to the third side.
b, c, ma One Solution (In Microsoft Word)
A GSP Sketch
2. Triangle given two sides and the median to one of those sides.
a, b, ma
3. Triangle given a side, an altitude to that side and a median to that side.
a, ha, ma
4. Triangle give a side, the altitude to that side and the median to a different side
a, ha, mc
GSP file for demonstration
5. Triangle, given a side, the angle opposite the side, and the radius of the incircle
a, A, r
6. Triangle, given a side and the altitudes to the other two sides.
a, hb, hc
7. Triangle, given a side, an altitude to another side, and the angle bisector to the third side.
8. Triangle, given two angles and the perimeter
A, B, a+b+c
9 . Triangle, given the three medians
ma, mb, mc
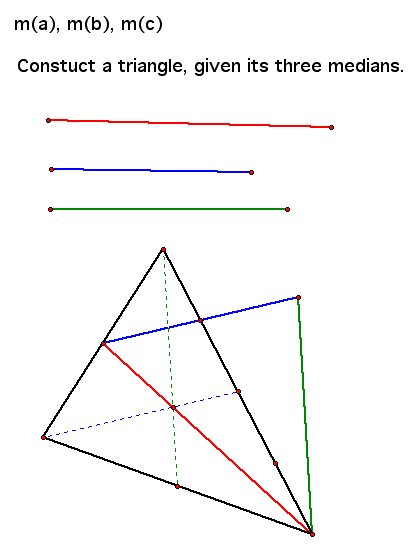
Click HERE for a GSP Sketch and Script tool
Note: The Script tool selected will allow you to provide three segments as input and will produce the corresponding triangle.
10. Triangle, given two sides and the angle opposite one of the sides
a, b, A
11. Triangle, given two sides and the altitude to the third
a, c, hb
12. Triangle, given a side, the median to that side, and another median
b, mb, ma
13. Triangle, given a side and the angle subtending (opposite of) that side, and a segment equal to the sum of the other two sides.
a, b+c, A
14. Triangle, given a side and the angle bisecting segments to the sides opposite each endpoint of the given segment.
a, db, dc
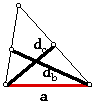
Show that this is an impossible construction with straightedge and compass.
15. Triangle, given the perimeter, an angle, and the altitude from that angle.
a+b+c, A, ha
16. Triangle, given a side, an angle adjacent to the side, and a segment equal to the sum of the other two sides.
a, B, b+c
17.
b+c, B, hc
18.
b+c, C, hb
19.
b+c, A, B
20.
b+c, a, hb
21.
ha, hb, hc
22. Creat other triangle construction problems.