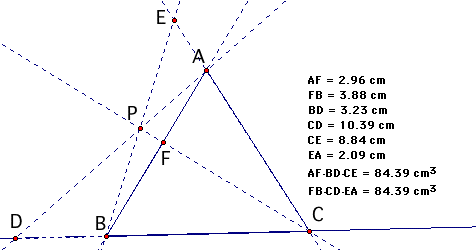
The GSP sketch alongside proves that our previous findings are not unique to when P is inside the triangle. When P is outside the triangle, we obtain some exterior proportions but the two products (AF)(BD)(CE) and (BF)(CD)(AE) are still equal.

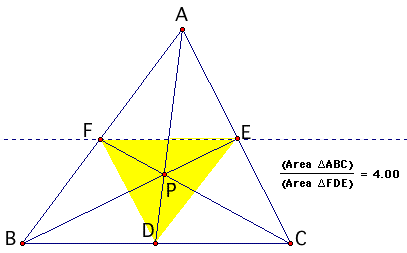
The ratio of the the areas of triangle ABC to triangle DEF will always be greater than or equal to 4. The ratio will be exactly equal to 4 when the segment joining E and F is parallel to the base BC and F bisects AB and E bisects AC. This will mean that CF, AD and BE are medians and P is the orthocenter. Let us prove this theorem RTP: area triangle DEF = 1/4 area triangle ABC Proof: Since F bisects AB and E bisects AC... 1) FE // BC 2) FE = half the length of BC and therefore FE = BD = DC Also remember that triangles with equal bases lying between parallel lines have equal areas. therefore area DEF = area BDF = area CDE Also perpendicular distance from A to FE is equal to perpendicular distance from D to FE. therefore area DEF = area AFE therefore area DEF = 1/4 area ABC Q.E.D.

Back to the First Proof Page

Back to the Main Final Project Page

Back to my Main Page