The topic for investigation here is going to be parametric equations. We will start by looking at some basic parametric equations and move on to some advanced parametric equations.

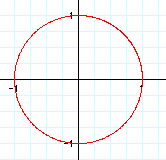
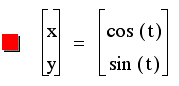We can see here that the parametric equations above represent another way of writing down the equation of a circle. We notice that the coefficients of both the sint and the cost is 1. The radius of the circle is also 1.

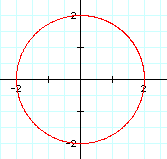
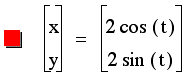When we change the coefficients of the sint and the cost to 2, the radius of the circle becomes 2 also.

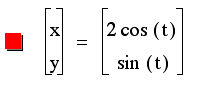When we vary the coefficients of sint and cost, the shape of the grap becomes an ellipse. Since the ellipse has x-intercepts of 2 and -2 when the coefficient of the cost is made 2, we suspect something...

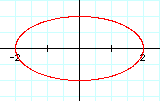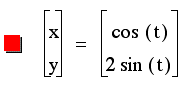As we suspected, the y-intercepts of the ellipse become 2 and -2 when the coefficient of the sint is made to be 2.

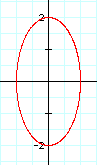Conclusion: The coefficients of the sin(t) and the cos(t) are the x- and the y-intercepts of the ellipse. Let us test our theory with one last example.

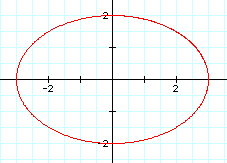
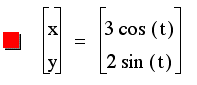As we suspected, when the coefficient of cost is 3, the x-intercepts of the ellipse is 3 and -3 and when the coefficient of the sint is 2, the y-intercept is 2 and -2.

Forward to the Second Parametric Equations Page

Forward to the Third Parametric Equations Page

Back to my Main Page