Construction of a Parabola in GSP
By: Diana Brown
Construct a parabola given a fixed
point for the focus and a line (segment) for the directrix:
a. Use an Action Button to
generate the parabola from an animation and trace of a constructed point.
b. Repeat 9a with a trace of the
tangent line at the constructed point.
c. Some explorations
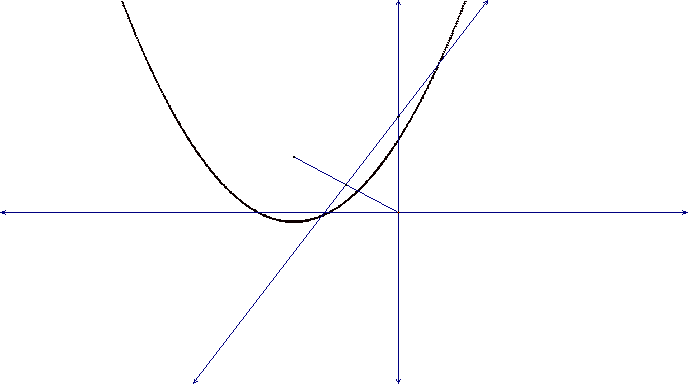
Definition: A parabola is the set of all points in a plane such
that the distance from these points to a fixed point, the focus, is equal to
the distance from the set of points to a fixed line called the directrix. The
axis of the parabola is the line through the focus and perpendicular to the
directrix. A point on the axis and halfway between the focus and the directrix
is called the vertex.
Using
this definition you can construct a parabola in Geometerís Sketchpad (GSP).
First
draw a line which will be the directrix. Then plot a point somewhere not on the
directrix, this will be the focus. Since a parabola is the set of points equidistant from the
directrix the focus, we will create a point on the directrix and a segment
between this point and the focus and find a perpendicular bisector between
these two points.† Next construct a
perpendicular to the point on the directrix. Where these two lines intersect
will be the traces of the parabola.
A) Click on the below picture to open the GSP file so you
can animate the sketch to see how the parabola was created.
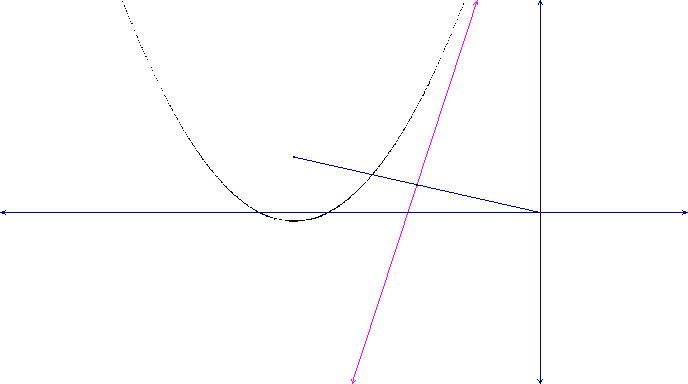
B) The next sketch is the same construction but
tracing the tangent line to the parabola. Click on the picture below to open
the GSP file to explore tracing the tangent line.
C) Some explorations with these parabolas:
What happens when I move the focus point further away from the directrix or
closer to the directrix.

It seems that when you move the focus closer to the
directrix the parabola is narrower than before,
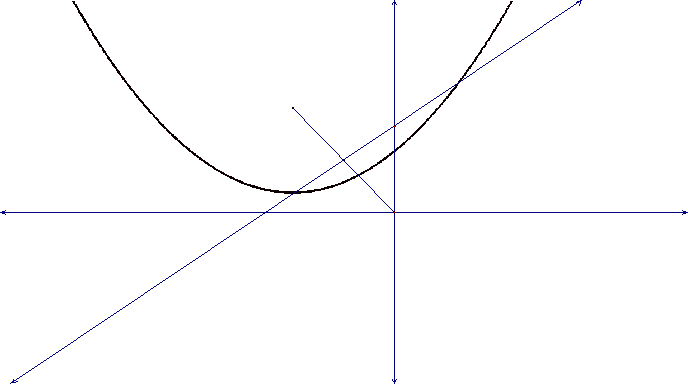
And when you move the focus further from the
directrix the parabola is wider than before.
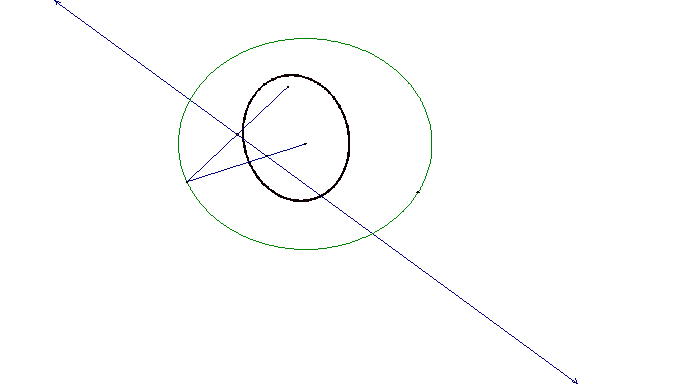
Now what would happen if the point moving about the
line called the directrix was moving around a circle instead of a line?
To construct this:†
I created a circle and point on the circle and inside the circle not
lying on the circle itself. I created a segment between these two points and
its perpendicular bisector.† Where the
radius of the circle and the created perpendicular bisector intersected is what
I traced to create a locus of points that formed an ellipse.
Click on the above picture to open the GSP file to
explore.