The Centers of a Triangle
By: Diana Brown
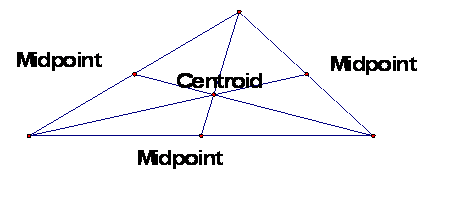
The CENTROID of a triangle is the common intersection of the
three medians. A median of a triangle is the segment from a vertex to the
midpoint of the opposite side.
Click on the picture to open the
GSP file to explore what happens to the figure as you drag one of the vertices.
Notice that the centroid is always
on the inside of the circle.
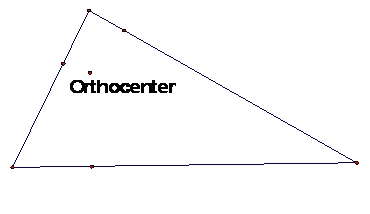
The ORTHOCENTER of a triangle is the common intersection of the
three lines containing the altitudes. An altitude is a perpendicular segment
from a vertex to the line of the opposite side.
Click on the first picture to open
the GSP file to explore what happens to the figure as you drag one of the
vertices.
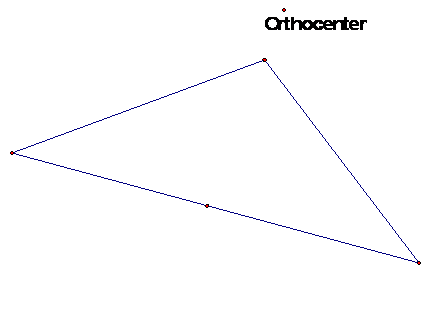
Notice that the orthocenter is
sometimes outside the triangle, sometimes on the triangle, and sometimes inside
the triangle.
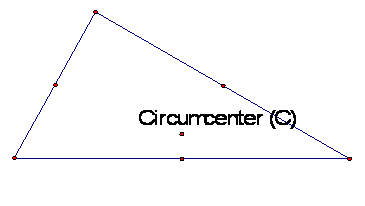
The CIRCUMCENTER of a triangle is the point in the plane
equidistant from the three vertices of the triangle. Since a point equidistant
from two points lies on the perpendicular bisector of the segment determined by
the two points, the Circumcenter is on the perpendicular bisector of each side
of the triangle.
Click on the first picture to open
the GSP file to explore what happens to the figure as you drag one of the
vertices.
Notice that the Circumcenter is
also sometimes outside the triangle and sometimes inside the triangle.
The INCENTER of a triangle is the point on the interior of the
triangle that is equidistant from the three sides. Since a point interior to an
angle that is equidistant from the two sides of the angle lies on the angle
bisector, then the Incenter must be on the angle bisector of each angle of the
triangle.
Click on the picture to open the
GSP file to explore what happens to the figure as you drag one of the vertices.
Notice that the Incenter stays
inside the triangle.
Summary Table:
|
|
Concurrent |
Inside/Outside/On the Triangle |
||
|
Center |
Lines |
Acute |
Right |
Obtuse |
|
Centroid |
Medians |
inside |
inside |
inside |
|
Orthocenter |
Altitudes |
inside |
on |
outside |
|
Circumcenter |
Perpendicular bisectors of the sides |
inside |
on |
outside |
|
Incenter |
Angle Bisectors |
inside |
inside |
inside |