---

Altitudes and Orthocenters

By: Diana Brown

---

1. Construct any triangle ABC and 2. Construct the Orthocenter H of triangle ABC.

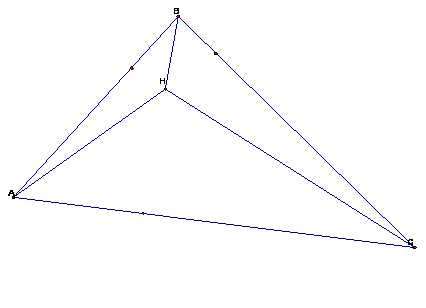
3. Construct the Orthocenter of triangle HBC.

Notice that the Orthocenter of triangle HBC is the vertex A of triangle ABC

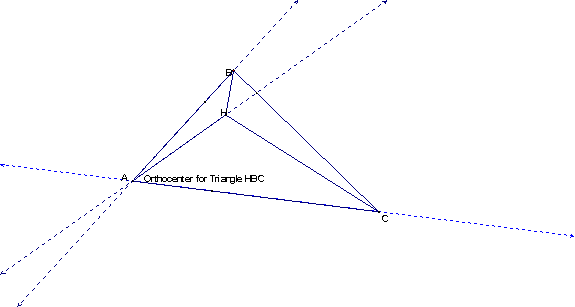
4. Construct the Orthocenter of triangle HAB.

Notice that the Orthocenter of triangle HAB is the vertex C of triangle HAB

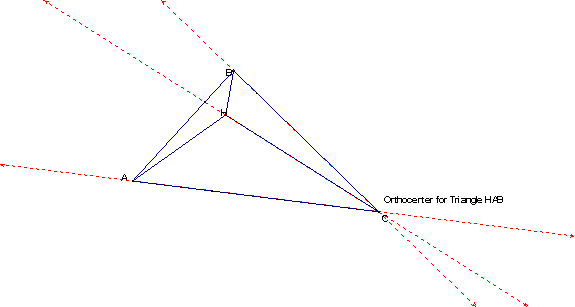
5. Construct the Orthocenter of triangle HAC.

Notice that the orthocenter of Triangle HAC is vertex B of Triangle ABC

This remains true if you change the shape of any of the triangles:

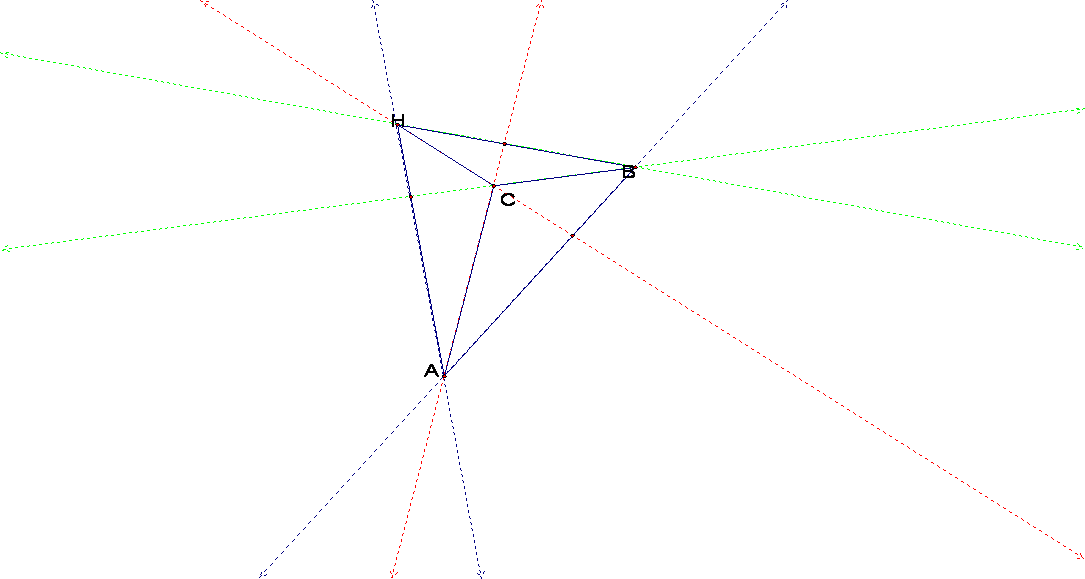
6. Construct the Circumcircles of triangles ABC, HBC, HAB, and HAC.

Now let’s move around some of our vertices of our original triangle ABC.

Lets see how the diagram would change if A is moved to where the orthocenter H is.

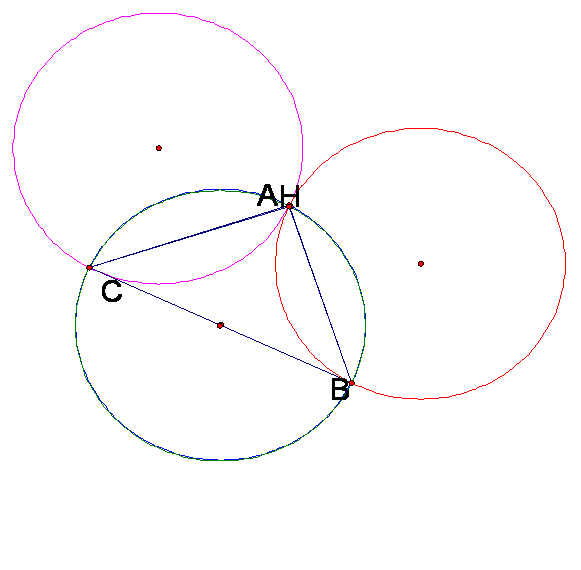
We can see that our Circumcircles for HBC and ABC are now the same because triangles HBC and ABC are now the same.

Lets see if this holds true by moving another vertice to H. Lets move B to the orthocenter H of original triangle ABC

Yes the conjecture holds true

---

To further manipulate the above diagrams to come up with your own conjectures click here for the GSP file.

---

Return to My Homepage

---