Assignment 4: Similar Triangles

by
Tom Cooper

I set out to do problem #8, but I would like to report on a variation.

8. Take an acute triangle ABC. Construct H and the segments HA, HB, and HC. Construct the midpoints of HA, HB, and HC. Connect the midpoints to form a triangle. Prove that this triangle is similar to triangle ABC and congruent to the medial triangle. Construct G, H, C, and I for this triangle. Compare.

Instead of letting H be the Orthocenter of ABC, I started with the circumcenter. Since I use C in my triangle ABC, I refer to the circumcenter by H.

I then constructed the circumcenter H and the segments HA, HB, and HC. I constructed the midpoints of HA, HB, and HC, and I connected the midpoints to form a triangle.

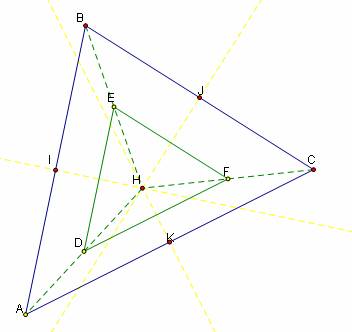
It appears that triangle ABC is similar to triangle DEF. Is it?

Claim: Triangle ABC is similar to triangle DEF

Proof  (Using Classical Euclidean Geometry):

1.  Angle AHC = Angle DHF                            1. They are the same angle.

2.  (AH)/(DH) =(HC)/(HF)=2 2. D and F are midpoints of AH and HC, respectively.

3. Triangle AHC is similar to Triangle DHF     3. SAS

4. Angle HAC = Angle HDF   and                    4. Corresponding angles of similar triangles.

    Angle HFD = Angle HCA

A similar argument shows that triangle ABH is similar to triangle DEH and triangle BHC is similar to triangle EHF.

Thus, by corresponding parts of similar triangles, angle BAH = angle EDH, angle ABH = angle DEH, angle HBC = angle HEF, and angle BCH = angle EFH.

Thus we have,

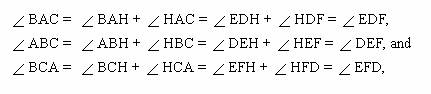
Therefore, triangle ABC is similar to triangle DEF by AAA.  

Note that this proof will hold even when H is not inside of triangle ABC.

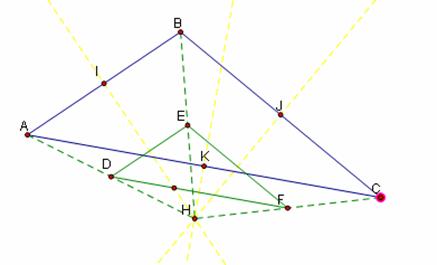
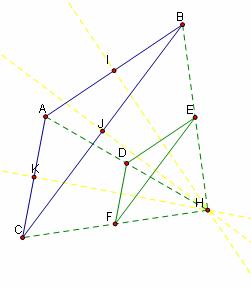
In fact, the proof will hold even when H is not the circumcenter. That gives the following generalization:

Claim: Given a triangle ABC and any point H, construct the segments HA, HB, and HC. Then construct the midpoints of HA, HB, and HC and construct a triangle with these three midpoints as vertices. Then the resulting triangle will be similar to triangle ABC with one forth of the area.

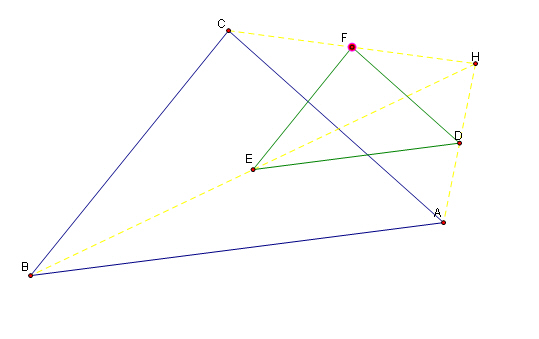
Explore this yourself with Geometer's Sketchpad.

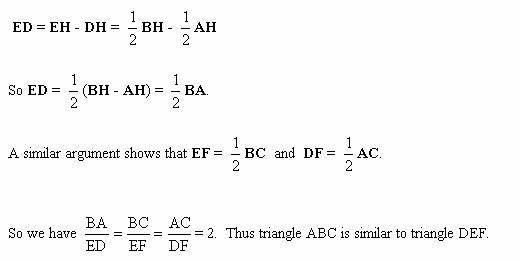
I will use bold letters and endpoints to indicate vectors. For example BA is the vector from B to A.

Proof (Using Vector Algebra):

By vector addition, we have

BA + AH  = BH        and       ED + DH = EH                                  

or equivalently,

BA = BH - AH         and        ED = EH - DH

Since E and D are the midpoints of BH and AH respectively, we have