
Assignment 7: Tangent Circles
by
Tom Cooper
The question that we are going to explore in this assignment
is, "Given two circles, can we find a third circle that is tangent to each
of them?" To accomplish this, we will use the dynamic power of Geometer's
Sketch Pad. This will allow us to construct a single case and change it into
other cases quickly.
To begin, we will examine the construction suggested by Dr. Wilson in the
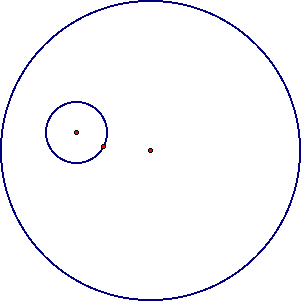
assignment page. Consider two circles with a smaller circle completely inside
of a larger circle.
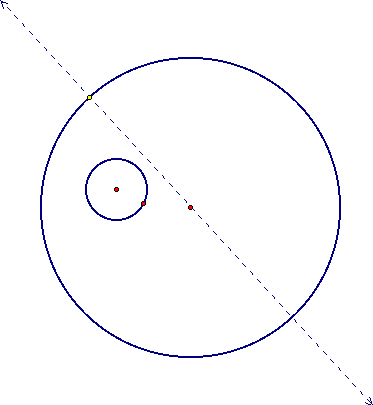
Suppose that we know a point on the larger circle that we want to be the intersection of a tangent circle. We can construct a line from the center of the larger circle to this point.
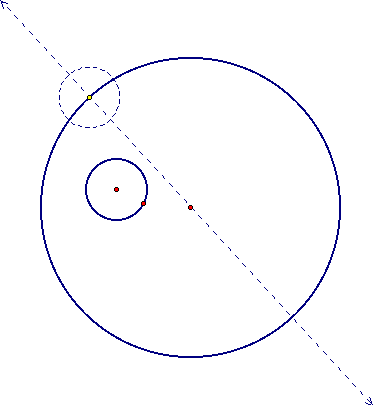
Now suppose that we create a copy of the smaller circle, centering it at the desired intersection point.
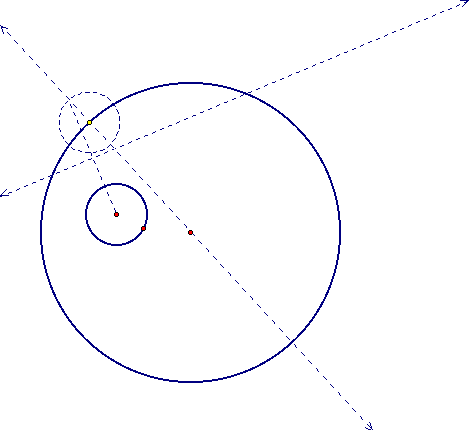
Now construct a segment from the center of the small circle to the upper intersection of the copy with the dashed line from the center, and construct its perpendicular bisector.
If we connect the intersection of the lines with the radius
of the smaller circle, we get an isosceles triangle. Furthermore, it should be
apparent that the intersection of the lines is equidistant from the
intersections of the isosceles triangles and the original circles.
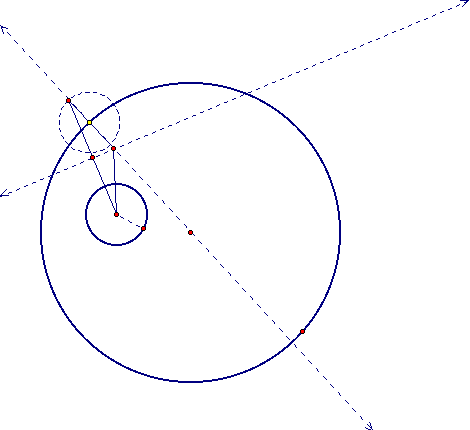
So the intersection of the line through the center of the larger circle and the perpendicular bisector of the base of the isosceles triangle is a good candidate for the center of a tangent circle. So, let's draw it.
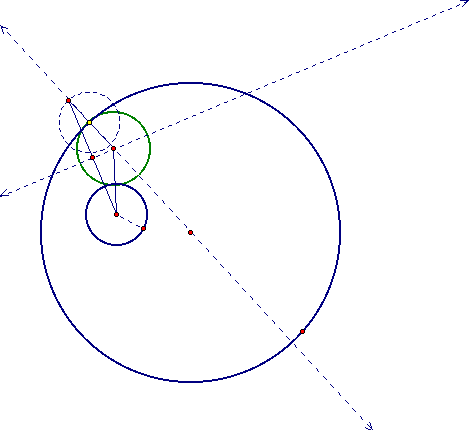
The dynamic power of GSP allows us to drag the tangency point on the larger circle around and see many different tangent circles. We can even animate this action and trace the locus of the center of the tangent circle. It gives us an ellipse as seen below.
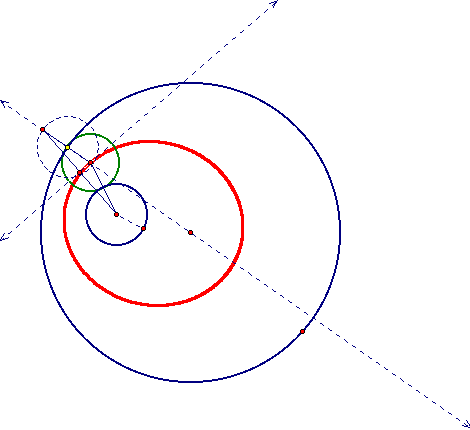
For a script tool and the animation, click here.
Are these the only possible circles that are tangent to both of the original circles? Consider the following construction.
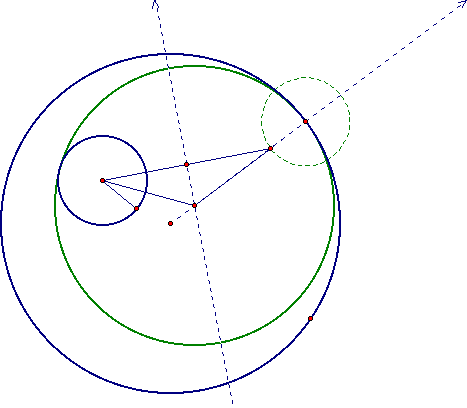
Here we have a tangent circle that contains the smaller circle. Again, we can animate the tangent point of the larger circle and trace the locus of the center of the tangent circle. What do you think this locus will look like? Click here for the script and script tool.
Can you create your own constructions where the known tangent point is on the smaller circle?
Click here and here for examples.
Now consider what would happen if the two circles intersected.
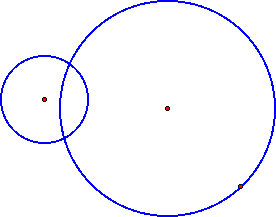
We can do the same type of construction as before.
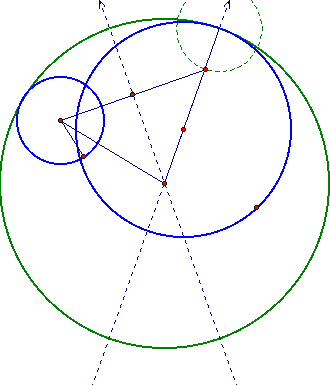
The above picture shows the case where the tangent contains the smaller circle (initially). Can you do the other case?
What is the locus of the center of the tangent circle now?
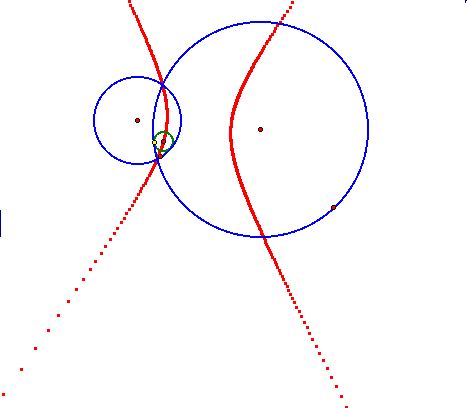
Now it is a hyperbola. Did that surprise you? See if you can find another case. To explore this case more, click here.
What other cases could you try? What other arrangements could you make with the original circles besides these two?
Here is one more example: Disjoint 1
Did you come up with this or others?