Proof of Triangle Angle Sum

by Kristina Dunbar, University of Georgia

and Michelle Corey, Russell Kennedy, Floyd Rinehart, UGA

Triangle Angle Sum:

The sum of the interior angles of a triangle is 180º.  More precisely, if A, B, and C are distinct points, then a(ACB) + a(CBA) + a(BAC) = 180.

Proof:

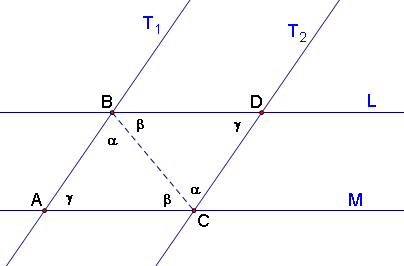
Let's start with the given points A, B, and C.  We can construct a line M through points A and C, then a line at point B that is parallel to AC, called L.  We can do this by the existence of parallel lines.  Then, by the line axiom, we can create a line T₁ going through points A and B, and a line parallel to T₁ at C, called T₂.  This gives us the point D, the intersection of T₂ and L.  Now we have two sets of parallel lines:  T₁||T₂ and L||M. 

We know that γ + (α + β) = 180º because they are the same side interior angles of the transversal T₁ that crosses L and M. 

Then we can look at parallel lines T₁ and T₂ and see that α (angle ABC) = α (angle BCD) because of alternate interior angles.  See picture above.

However, we also know that when we look at parallel lines T₁ and T₂ where M is the transversal, that same side interior angles must be supplementary, i.e. = 180º.  Then we know that the β's must be the same, because we will get that (α + β) + γ  = 180º.  Now look at triangle ABC, where the three angle measurements are α, β, and γ, so the sum of the interior angles of a triangle is 180º.

|| Parallels Main Page || Kristina Dunbar's Main Page || Dr. McCrory's Geometry Page ||