

Part 1: Construction of a Triangle with its Orthocenter. Using the altitudes of the initial triangle, construct smaller triangles inside and locate their Orthocenters.
Lets recall what an altitude of a triangle is by defining the altitude of a triangle as a line which is perpendicular to a side and goes through that side's opposite vertex. The altitude is sometimes called the height of the triangle.
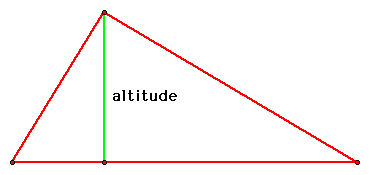
Now lets construct the Orthocenter. This is done by first finding the remaining two altitudes of our triangle. The Orthocenter is the intersection of these three altitudes. We will label the Orthocenter H.
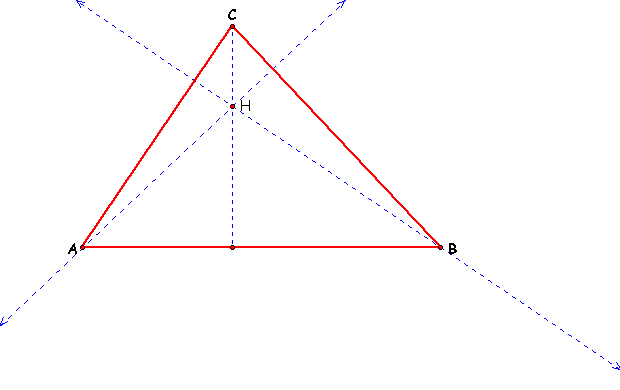
Now, as you can see below, the altitudes of triangle ABC makes three new inner triangles: AHC, AHB, and BHC.
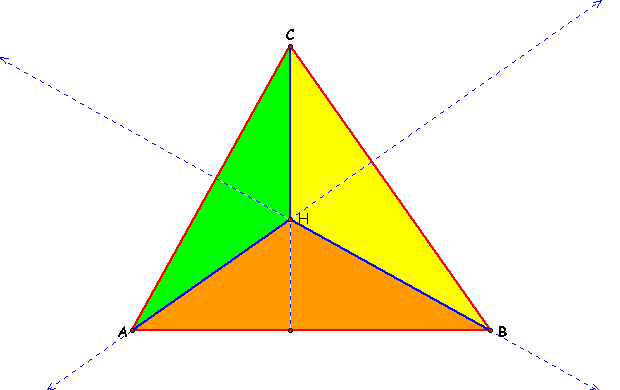
Using these three new triangles we will construct their individual Orthocenters.
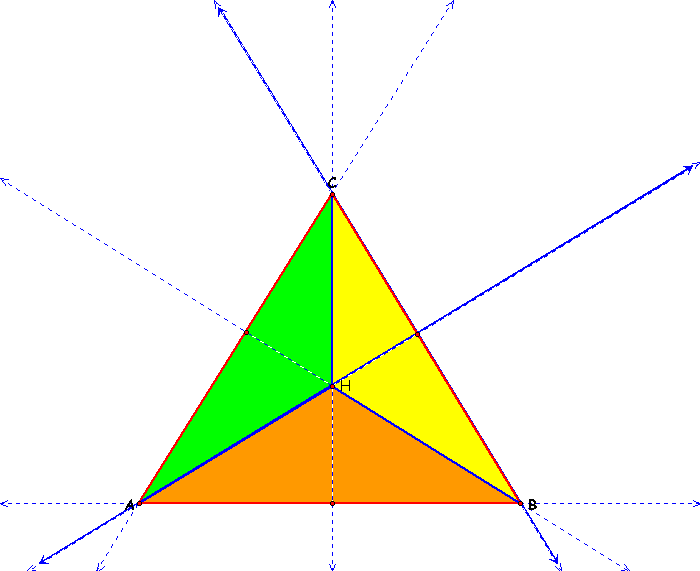
You may notice that the Orthocenters on the new triangles lie on the sides of the original ABC triangle!
For argument sake, lets change the shape of ABC. We should see that the change does not effect the Orthocenters.
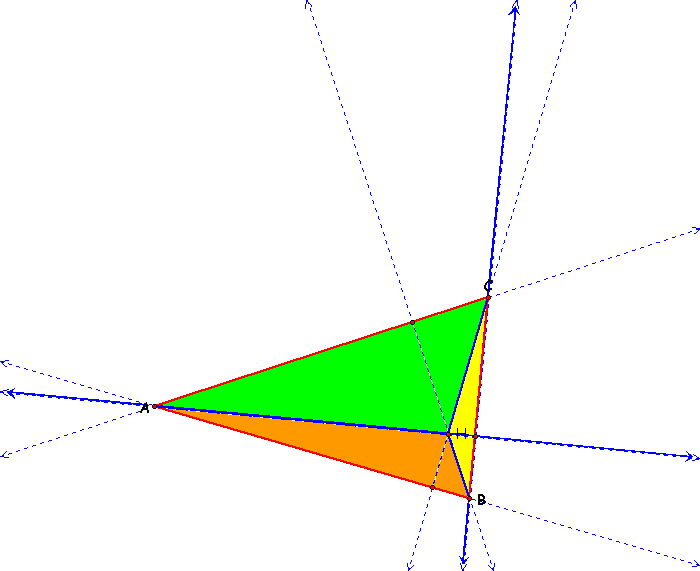
Just as we thought, the centers have not changed.
If you want to try manipulating this construction click on ABC to open a the GPS construction.
Part 2: Construct the internal angle bisectors of a triangle which are extended to meet the circumcircles at three points.Explore the relationship of angles created.
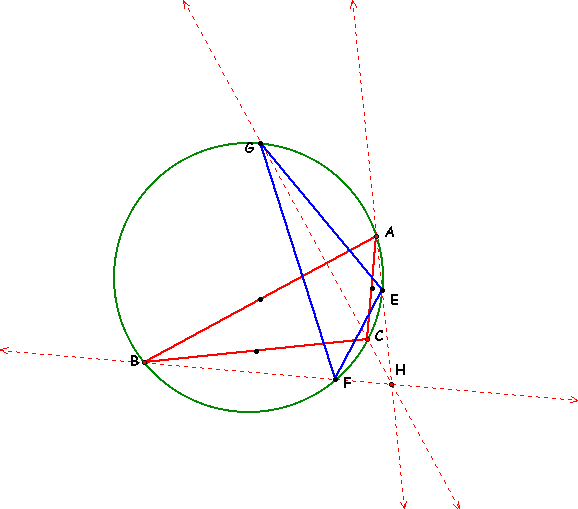
We will begin by constructing a triangle ABC and finding its Orthocenter and its Circumcenter. Having done that we will lay in the circle with its center being the Circumcenter of ABC.
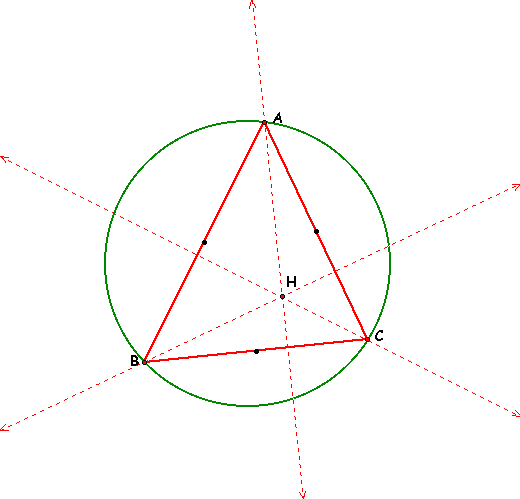
Now we find the points of intersection of our lines we created constructing the Orthocenter and our circle. A new triangle is formed.
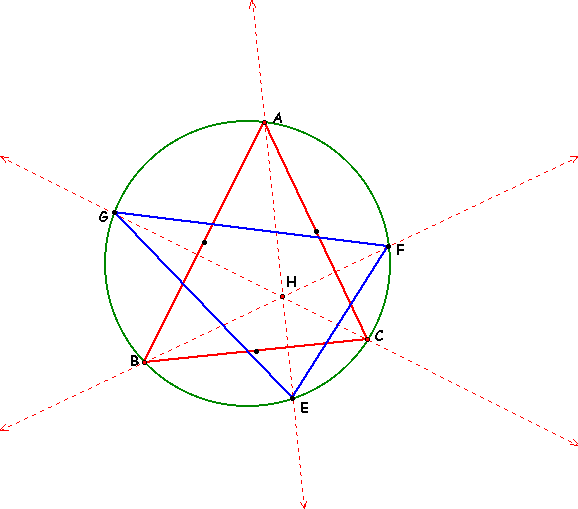
We now want to explore the relationship between the angles of EFG in terms of ABC.
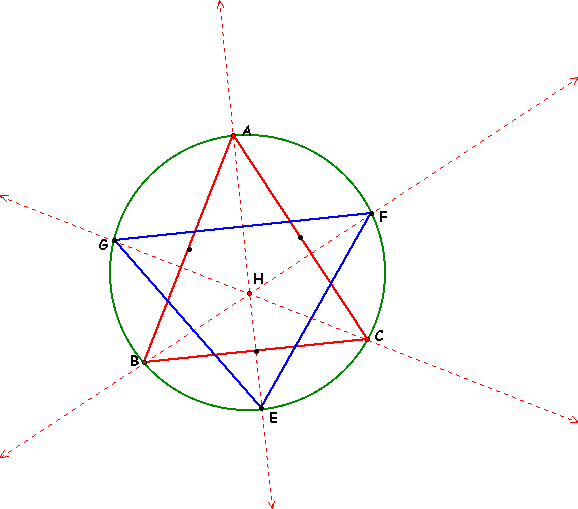
By making ABC an equilateral triangle, where each angle is 60 degrees, we can see that our Orthocenter lines are also intersect the vertices of EFG. That is, EFG is also equilateral. Now in the following two examples lets make ABC 1.) acute and 2.) obtuse.
1.)
2.)
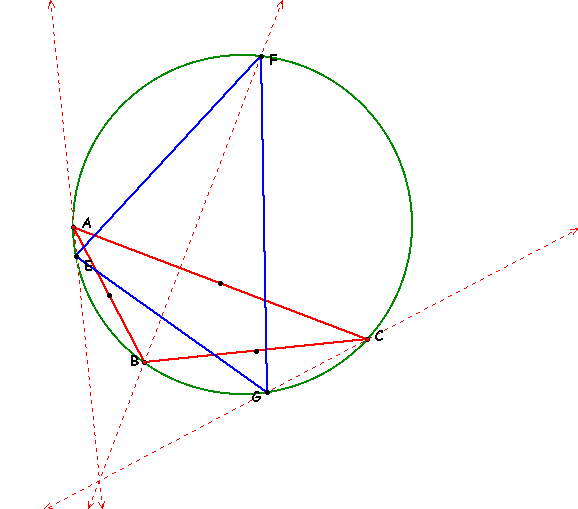
Again, if you would like to manipulate this construction click on Circumcenter to open the GPS construction.