Investigate the following equation when

for various values of a and b.

Let's take a look at the equation

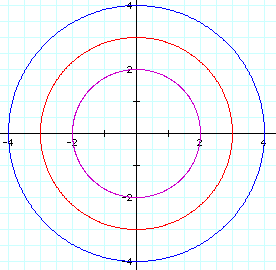
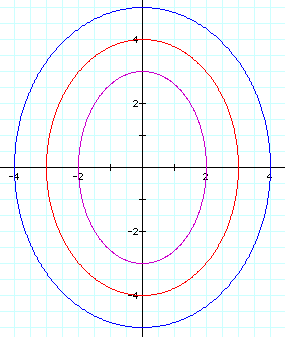
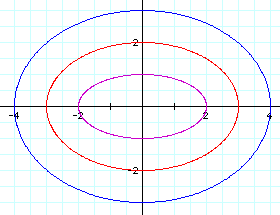
when a = b, a < b, and a > b.

a = b

a < b

a > b

In this case, it is easy to see that when a=b, the outcome is a circle with its center at the origin. The radius of the circle is determined by the value of a and b. In other words, as a and b increase, the radius of the circle also increases. Actually, more specifically, a = b = the radius of the circle.

When a < b, what you get is an eclipse with its center at the origin. In this eclipse, a determines the width and b determines the height.

Similarly, when a > b, you also get an eclipse with its center at the origin. In this case, like the previous one, a also determines the width and b determines the height. So, this eclipse is rotated 90 degrees in relation to the previous case.

Let's look at some other cases of values of a and b, keeping one of the values constant while the other increases.

a = 1, while b increases a=1, b=1 a=1, b=3 a=1, b=2a=1, b=4 a=1, b=5

b = 1, while a increases a=1, b=1 a=3, b=1 a=2, b=1 a=4,b=1 a=5, b=1

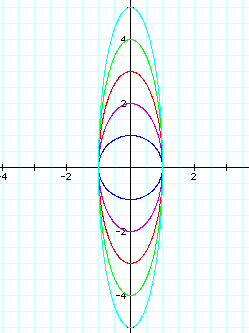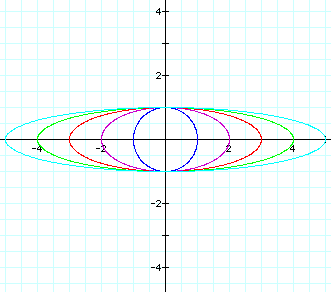Again, we can see that when a = b (blue graph above), a circle is formed with radius equal to a and b.

Keeping a constant at 1 and increasing b, we see an eclipse that has a minor axis which remains constant along the x-axis, and a major axis that increases along the y-axis as b increases. The x-intercepts remain 1 and -1, or more generally a and -a. The y-intercepts are always b and -b.

The second graph above follows the same pattern, only this time b remains constant at 1. So, in this case, the minor axis is along the y-axis and remains constant. The major axis is along the x-axis and increases as a increases. The x-intercepts are a and -a, and the y-intercepts are 1 and -1 (or b and -b).

Return