Investigate for different values of a, b, and k.

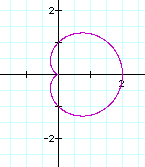
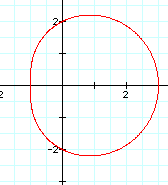
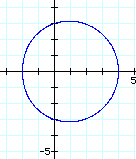
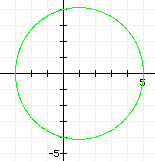
First, let's look at the graphs as a changes.

a=1, b=1, k=1

a=2, b=1, k=1

a=3, b=1, k=1

a=4, b=1, k=1

a=5, b=1, k=1

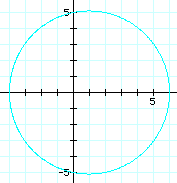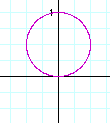
As a increases, a circle begins to form. Finally, at a > or = 3, we have a circle. The center is always at (1, 0) and the radius is equal to the value of a.

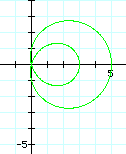
What happens as b changes?

a=1, b=1, k=1

a=1, b=2, k=1

a=1, b=3, k=1

a=1, b=4, k=1

a=1, b=5, k=1

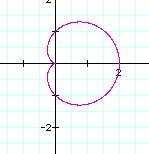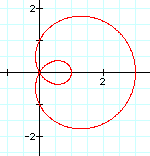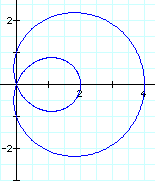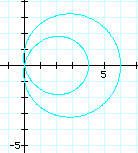It seems that as b changes, our loop just gets bigger. In fact, when b = 2 or anything greater, there are actually 2 loops (one inside and one outside).

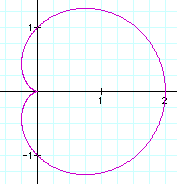
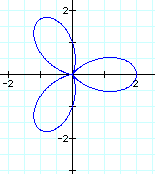
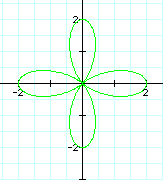
Now, let's take a look at what happens as k changes and a = b remains constant.

a=1, b=1, k=1

a=1, b=1, k=2

a=1, b=1, k=3

a=1, b=1, k=4

a=1, b=1, k=10

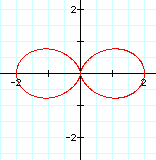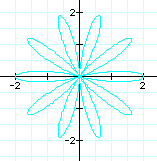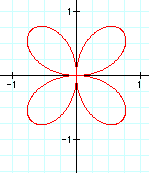
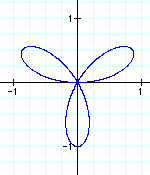
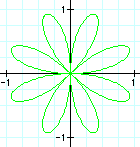
When a and b are equal and k is an integer, as in this case, this is one version of the n-leaf rose. The value of k determines the amount of petals. It appears that the domain and range are always between 2 and -2.

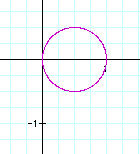
Let's compare this with the equation . What happens as k changes?

b=1, k=1

b=1, k=2

b=1, k=3

b=1, k=4

b=1, k=10

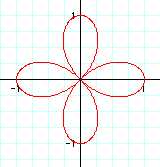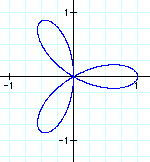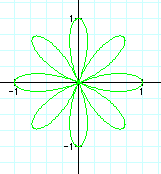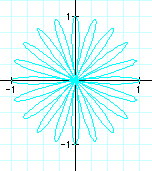These graphs appear to be quite similar to the previous ones. However, in this case, the domain and range are always between 1 and -1. When k = 1, we get a circle with diameter 1. As k increases, so does the amount of pedals. When k is an even integer, the number of pedals is double the value of k. However, when k is odd, k = the number of pedals.

What happens if we replace cos by sin? Now, we have . What happens with the graph of this equation as k changes?

b=1, k=1

b=1, k=2

b=1, k=3

b=1, k=4

b=1, k=10

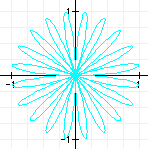These graphs very much resemble the graphs above. Notice how the graphs are the same, only rotated around the axes a bit.

Return