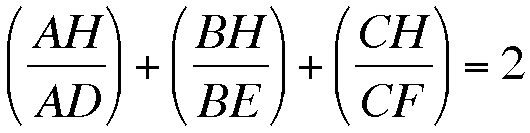Given triangle ABC. Construct the Orthocenter H. Let points D, E, and F be the feet of the perpendiculars from A, B, and C respectfully. Prove:
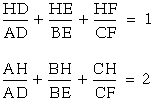
What if ABC is an obtuse triangle?
Given triangle ABC, we have constructed the orthocenter H and points D, E, and F such that D, E, and F are the feet of the perpendiculars (altitudes) of A, B, and C respectfully.

Then to show
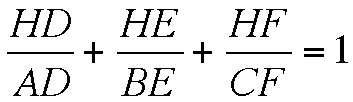
let's begin by identifying equivalents of the area of triangle ABC that we will need later.
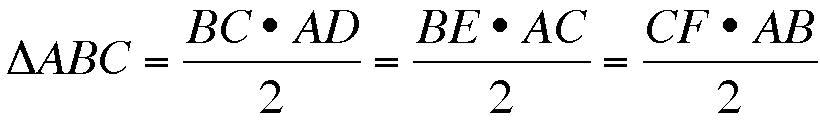
Now, consider ways we can transform the equation
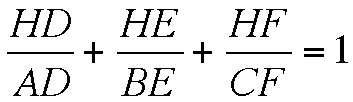
by utilizing the information we already know. Let's perform the mathematical manipulation of multiplying by 1.
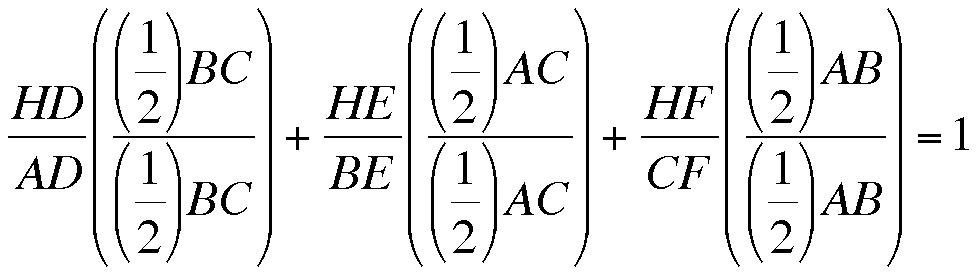
Now, we can notice that
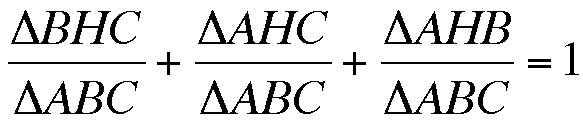
which is equivalent to
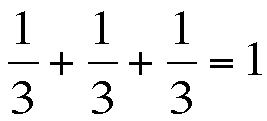
Therefore
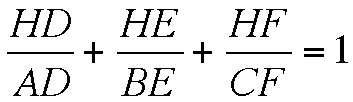
Next, we need to show
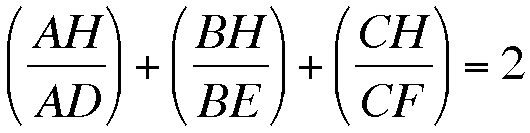
Now, we can perform substitutions for each of the numerators of each ratio.
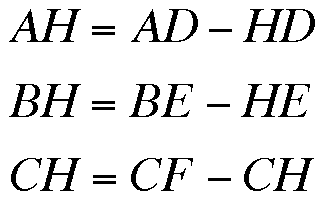
Then,
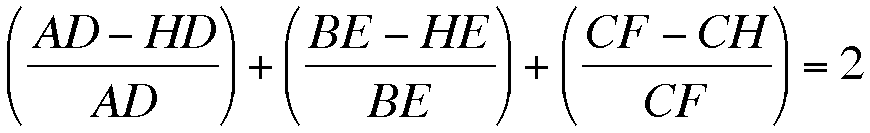
and
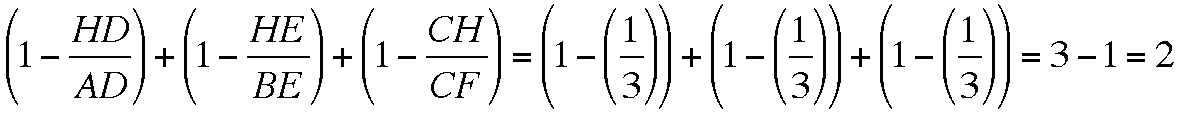
Therefore,