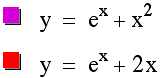Now that we have explored derivatives, we can now progress to the rules of differentiation. These rules are simply formulas that instruct the learner how to compute derivatives depending on a given function.
The rule for the exponential function, e, is by far one of the easiest differentiation rules to remember. The rule is
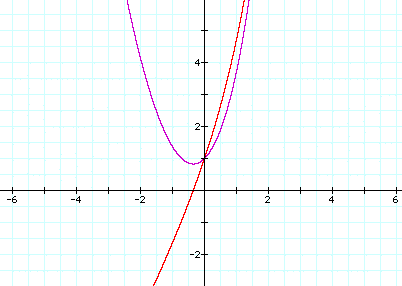
This says that the derivative of the exponential function is itself. That is, the slope of the tangent line to the exponential function at a point a, is equal to the y-coordinate at the point a.
The rule for the natural logarithmic furnction, ln, is also an easy derivative to recall. The rule is
This says that the derivative of the natural logarithm is the function 1/x. Below are some illustrations of above stated differentiation rules.
The following graph illustrates the function y=ln(4x) and its derivative y'=1/x.
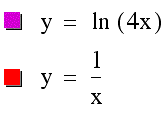
The following graph illustrates the function 
and its derivative 
