Angle Relationships in Circles

Objectives:  Have students discover three theorems concerning relationships of different angles of circles.

Lesson:

Have students discover the following theorems:

Theorem 1: If a tangent and a chord intersect at a point on a circle, then the measure of each angle formed is one half the measure of its intercepted arc. m<DAB = (1/2)mACB and m<EAB = (1/2)mAB
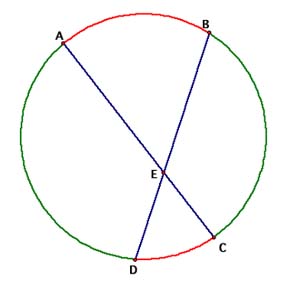
Theorem 2: If two chords intersect in the interior of a circle, then the measure of each angle is one half the sum of the measures of the arcs intercepted by the angle and its vertical angle. m<AEB = (1/2)(mAB + mCD) m< AED = (1/2)(mAD + mCB)
Theorem 3: If a tangent and a secant, two tangents, or two secants intersect in the exterior of a circle, then the measure of the angle formed is one half the difference of the measures of the intercepted arcs.
m<ADC = (1/2)(mCA - mBC)
m<EFG = (1/2)(mGHE - mEG)
m<IKM = (1/2)(mMI - mJL)

Here are the interactive GSP sketches of these theorems: Theorem 1, Theorem 2, Theorem 3.

Conclusion:  Discuss the activity with the students and have them describe the conclusions they were able to come to based upon the activity.  Review the theorems that the students should have discovered during their investigations.

Previous: Day 5
Next:  Day 7
Return to Homepage

Developed by Katherine Huffman