Angles Day 3 Answers

We know that two inscribed angles that intercept the same arc are equal in length, so the m<ADC = m<ABC = 52^o. We also know that the central angle is equal to twice the measure of the inscribed angle that intercepts the same arc, so m<AOC = 2(m<ABC) = 2(52^o) = 104^o.

2. Find the values for x and y and the measures of angle ABC, angle BCD, and angle DAB.

We know that opposite angles of a quadrilateral inscribed within a circle are supplementary, therefore we have that

m<ABC + m<CDA = 180^o
m<ABC + 112^o = 180^o
m<ABC = 180^o - 112^o
m<ABC = 68^o

Therefore, we must also have that m<BCD = (68 + 10)^o = 78^o giving us that

m<DAB + m<BCD = 180^o
m<DAB + 78^o = 180^o
m<DAB = 180^o - 78^o
m<DAB = 102^o

We know that if a tangent and a chord intersect at a point on a circle, then the measure of each angle formed is one half the measure of its intercepted arc. So we have that

m<DAB + m<BAE = 180^o
120^o + m<BAE = 180^o
m<BAE = 180^o - 120^o
m<BAE = 60^o

And now we can finally find mAB by saying that

m<BAE = (1/2)mAB
2(60^o) = mAB
120^o = mAB

We could also find mAB by knowing that the distance around a circle is 360o, therefore we must have that

mBAC + mAB = 360^o
240^o + mAB = 360^o
mAB = 360^o - 240^o
mAB = 120^o

We know that if two chords intersect in the interior of a circle, then the measure of each angle is one half the sum of the measures of the arcs intercepted by the angle and its vertical angle. So we have that

m<AEB = m<DEC = (1/2)(68^o + 55^o) = (1/2)(123o) = 61.5^o

mAB + mBC + mCD + mDA = 360^o
55^o + 74^o + 68^o + mDA = 360^o
197^o + mDA = 360^o
mDA = 360^o - 197^o
mDA = 163^o

m<DAE = m<BEC = (1/2)(74^o + 163^o) = (1/2)(237^o) = 118.5^o

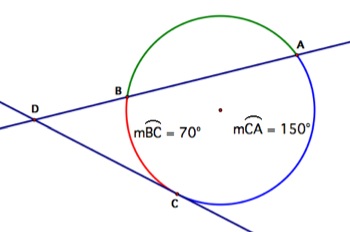
We know that if a tangent and a secant intersect in the exterior of a circle then the measure of the angle formed is one half the difference of the measures of the intercepted arcs. So we have that

m<ADC = (1/2)(mCA - mBC) = (1/2)(150^o - 70^o) = 80^o

We know that if two tangents intersect in the exterior of a circle then the measure of the angle formed is one half the difference of the measures of the intercepted arcs. So we have that

We also know that mBCA + mAB = 360^o so we have that mAB = 360^o - mBCA = 360^o - 265^o = 95^o. So now we can see that

m<ADB = (1/2)(mBCA - mAB) = (1/2)(265^o - 95^o) = (1/2)(170^o) = 85^o

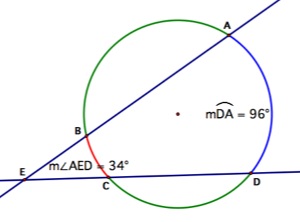
We know that if two secants intersect in the exterior of a circle then the measure of the angle formed is one half the difference of the measures of the intercepted arcs. So we have that

m<AED = (1/2)(mDA - mBC)
34^o = (1/2)(96^o - mBC)
2(34^o) = 96^o - mBC
68^o = 96^o - mBC
mBC = 28^o