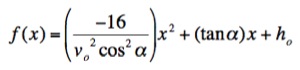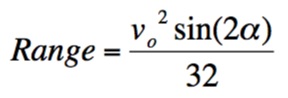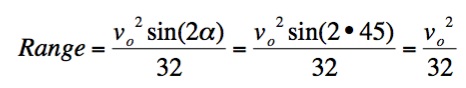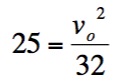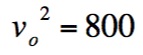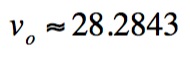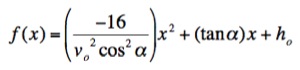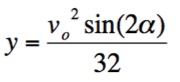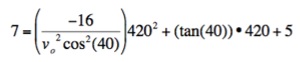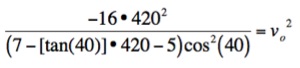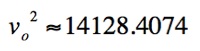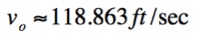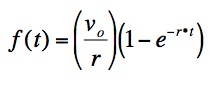Mathematics in Sports
Although not always realized, mathematics plays a very important role
in sports. Whether discussing a players statistics, a coaches
formula for drafting certain players, or even a judges score for a
particular athlete, mathematics are involved. Even concepts such
as the likelihood of a particular athlete or team winning, a mere case
of probability, and maintain equipment are mathematical in
nature.
Let's begin by looking at the throwing of a basketball. Now, we
can use the equation
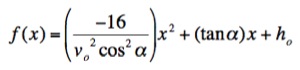
to help figure out the velocity at
which a basketball player must throw the ball in order for it to land
perfectly in the basket. When shooting a basketball you want the
ball to hit the basket at as close to a right angle as possible.
For this reason, most players attempt to shoot the ball at a 45o
angle. To find the velocity at which a player would need to throw
the ball in order to make the basket we would want to find the range of
the ball when it is thrown at a 45o angle. The formula
for the range of the ball is
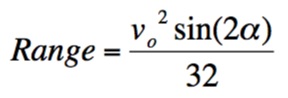
But since the angle at which the ball is thrown is 45o, we
have
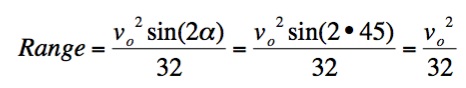
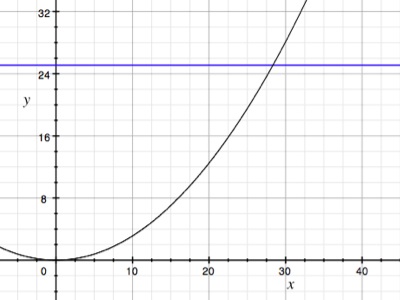
Now, if a player is shooting a 3 point shot, then he is approximately
25 feet from the basket. If we look at the graph of the range
function we can get an idea of how hard the player must throw the ball
in order to make a 3 point shot.
So, by solving the formula knowing that the range of the shot must be
25 feet we have
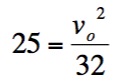
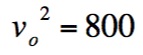
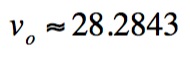
So in order to make the 3 point shot, the player must throw the ball at
approximately 28 feet per second, 19 mph.
Now let's look at the throwing and hitting of a baseball.
The pitcher wants to throw the ball so that he will strike out the
batter. If his throw is too high or low then it is a ball and the
better still has at least three more opportunities to hit the
ball. Similarly, when the batter hits the ball, he wants to hit
the ball so that it will be as far away from any of the other players
as possible if not outside of the ball field itself. The players
must take into consideration the speed and height of the ball to ensure
that they will throw or hit it properly. Here is the equation for
finding the projectile motion of a baseball will travel:
where all distances are measured in feet, ho is the height
from which the ball is thrown, α is the angle at which the ball is
thrown, vo is the speed at which the ball is thrown, and x
is the distance that the ball travels. We can find the distance
that the ball will travel by saying
Now, a batter would be more concerned with the range of the ball,
wanting it to travel far enough to allow him to at least make it to
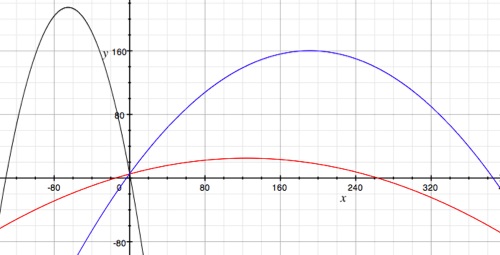
first base safely. Let's look at several graphs of the range with
different α's and a fixed vo and ho.
The black graph is when α = 30o, the blue graph when α = 45o,
and the red graph when α = 60o. So we can see from the
graph that an angle of 45o will send the ball the
furthest. So, a batter would want to hit the ball as close to a
45o angle as possible, while a pitcher, who is more concerned about the
ball veering off path, would want to throw the ball so the ball so that
it would travel as close to a straight line as possible.
Now, let's say it is approximately 420 feet from home plate to the edge
of a baseball field. The batter wants to hit the ball hard enough
so that it will travel out of the field, over the approximately 7 foot
wall at the back of the outfield. If the batter hits the ball at
a 40o angle and the ball is approximately 5 feet in the air
when struck, how hard must he hit the ball in order to have a
home run? Remember, that in the projection equation, f(x) is the
height of the ball, so now we have
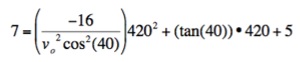
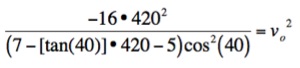
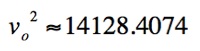
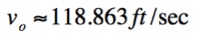
Therefore we have that the batter must his the ball at approximately
118 feet per second, which is approximately 81 mph, in order to hit a
home run when he hits the ball at an angle of 40o.
We could also look at a sport such as bowling which many people
consider to be quite simplistic. However, you must consider the
angle of the ball and the velocity with which the ball is thrown when
trying to get a strike. The path of a bowling ball, thrown in a
straight line, can be represented by the following equation:
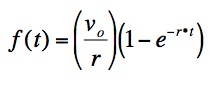
where vo is the velocity of the ball, t is the time in seconds that the
ball travels, r is a constant represents the friction, and g(t) is the
distance in feet that the ball travels after t seconds.
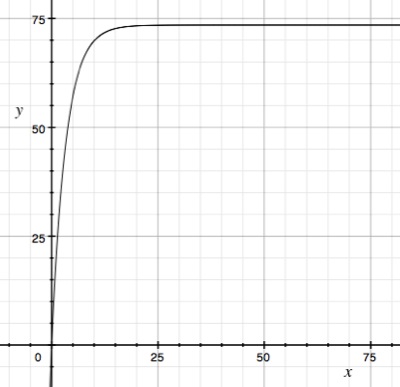
Now, the length of a blowing lane is approximately 60 feet. Let's
say that the friction caused by the bowling ball on the slick surface
of the bowling lane is approximately 0.3 and the ball is rolled at
approximately 15 mph, or 22 feet per second. Now if we graph this
equation we have
So we can see that the bowling ball, if thrown at 15 mph, should make
it all the way down the bowling lane.
Mathematics is also used in ranking players and determining playoff
scenarios. From something as simple as using a matrix to the
formulas used to determine a players or teams statistics, mathematics
is an integral part of this system. For example, in the olympics,
most sports have players draw numbers to see who they will be competing
against. If there are 2k contestants then all athletes
participate in the first round of play, if not, then some of the
participants enter during the second round of play. The number of
athletes entering during the second round of play will be
2k - n, where n is the number of contestants. Rankings
are also an important aspect of sports. In sports such as tennis,
when rating athletes, an integral estimator is used which is based on a
players performance in a series of matches over a certain period of
time. Even horse racing uses mathematics to rank the horses based
on how well the have performed in previous matches, and these rankings
go into determining the value of a horse when a bet is placed.
Mathematics is very prevalent in sports, from the most complex of
formulas to the simplest ideas such as betting.
Return to Homepage