Napoleon's Triangle

Napoleon's Theorem states that given any triangle ABC you can construct an equilateral triangle on each side of the triangle ABC such that the figure formed by connecting the centroids of the three equilateral triangles is an equilateral triangle.  This equilateral triangle is called Napoleon's triangle, named after Napoleon Bonapart.  It is thought that either Napoleon himself discovered this triangle since it is known that he had a great interest in mathematics, or that a close friend discovered this triangle and named it for him.  Now we will look at Napoleon's triangle and prove that it is indeed an equilateral triangle.

Let's begin with triangle ABC.
Now we will construct three equilateral triangles, one on each side of triangle ABC.
Next we will find the centriods, the center, of each of the three equilateral triangles.

Finally we will connect these three points to form our triangle.  The yellow triangle is known as Napoleon's Triangle.

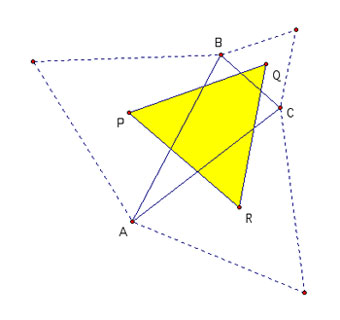
From looking at the above figure we can see that it appears that Napoleon's Triangle is indeed equilateral, now we will prove this to be a fact.

We know that m<QBC=30^o since triangle BEC is an equilateral triangle and BQ is an angle bisector.  Now we can apply the law of cosines to get:
      (PQ)² = (BC)² + (BA)² - 2(BC)(BA)cos(B + 60^o)
But we know that the centroid of a triangle is on the median of the triangle, ²/₃ the distance from the vertex, so we have that
      (BQ) = [^{(2/₃)sqrt(3)}/₂](BC) = ^(BC)/_sqrt(3)
      (BP) = [^{(2/₃)sqrt(3)}/₂](BA) = ^(BA)/_sqrt(3)
So now we can say that
      3(PQ)² = (BC)² + (BA)² - 2(BC)(BA)cos(B + 60^o)
Now we can look at triangles BAE and EAC and using the law of cosines we can express AE as
      AE = (BC)² + (BA)² - 2(BC)(BA)cos(B + 60^o)
   or
      AE = (AC)² + (BC)² + 2(AC)(BC)cos(C + 60^o)
Giving us that
      (BC)² + (BA)² - 2(BC)(BA)cos(B + 60^o) = (AC)² + (BC)² + 2(AC)(BC)cos(C + 60^o)
But we know that
      3(PQ)² = (BC)² + (BA)² - 2(BC)(BA)cos(B + 60^o)
And similarly,
      3(QR)² = (AC)² + (BC)² + 2(AC)(BC)cos(C + 60^o)
Therefore we must have that PQ = QR
And by looking at triangles ACD and ABD we can get that QR = RP
Therefore we have that PQ = QR = RP so Napoleons triangle is infact an equilateral triangle.

To view an interactive GSP sketch of Napoleon's Triangle click here.