EMAT 6680 - Fall 2004

Assignment 10

Parametric Curves

_______________

By Keri Hurney

 

 

I chose to explore part 7 of assignment 10. The problem posed was as follows:

Write parametric equations of a line segment through (7,5) with a slope of 3. Graph the line segment using your equations.

 

It is simple enough to graph a line that will pass through the point (x = 7, y = 5) given a slope of 3. Using the standard equation for a line in the form of

y = mx + b

where m is the slope and b is the y-intercept.

____________________

 

We would have the equation

5 = (3x7) + b

5 - 21 = b

b = -16 (y-intercept)

____________________

 

Our line would cross the y-axis at -16. We have two points (7,5) & (0,-16) and a slope of 3. The slope-intercept form of our line is:

y = 3x - 16

 

See the line (y = 3x-16) on the graph below.

What about those parametric equations we are supposed to be finding?

 

We can use the equation we found from the slope/y-intercept form:

y = 3x - 16

to help us come up with parametric equations for this line.

 

First we can set

x = t

 

then substitute 't' in for 'x' and get the following:

t = x

y = 3t - 16

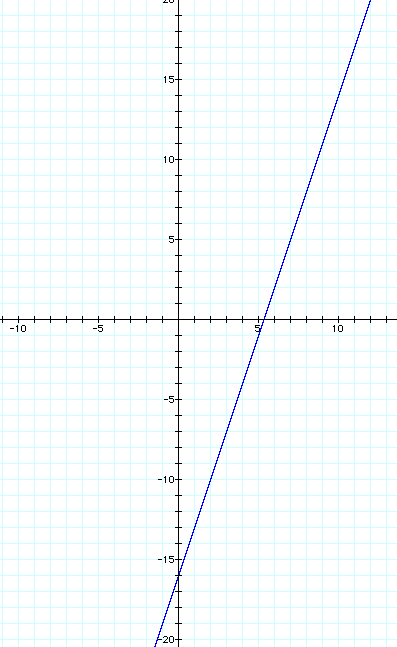
We now have our parametric equations for a line that passes through (7,5) with a slope of 3- see below for the graphical representation (t ranging from -20.. 20):

 

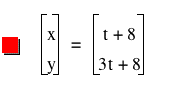
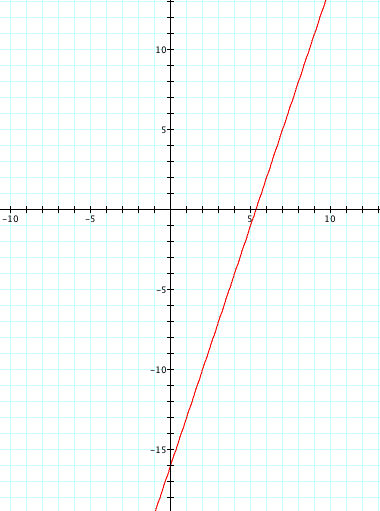
As the graph shows, this new line crosses the y-axis at -16, passes through (7, 5), and also has a slope = 3.

Return to Keri's Home Page