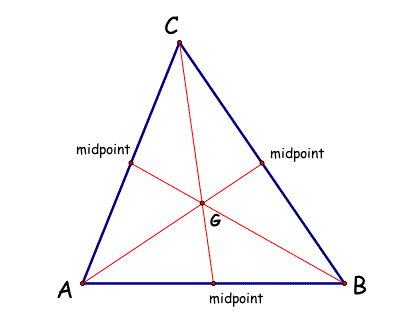
1. Centroid Script Tool
The Centroid of a triangle is defined as the common intersection of the three medians of a triangle, where a median of a triangle is the segment from the vertex to the midpoint of the opposite side.
Click on the triangle below to open a file in GSP with an example script tool (including instructions) that finds the Centroid of any given triangle. (The point, G, is the Centroid of the triangle ABC.)
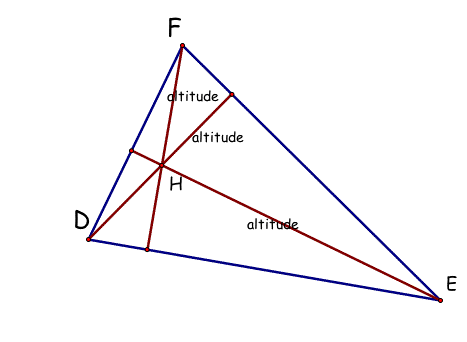
2. Orthocenter Script Tool
The Orthocenter of a triangle is found at the common intersection of the three altitude lines of a the triangle.
Click on the triangle DEF below in order to open GSP and use a script tool to create your own triangle with the Orthocenter.
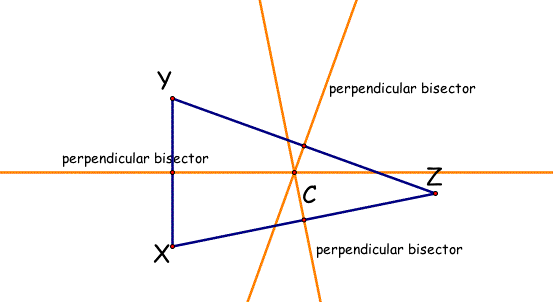
3. Circumcenter Script Tool
The Circumcenter of a triangle is the point in the plane equidistant from the three vertices of the triangle. In order to find the Circumcenter of a triangle, first find the three medians of the triangle and then use these median points to find the perpendicular bisectors of each side of the triangle. The intersection of the three perpendicular bisectors will be the Circumcenter.
Click on the triangle below to open GSP and use the script tool to create your own triangle showing the Circumcenter.
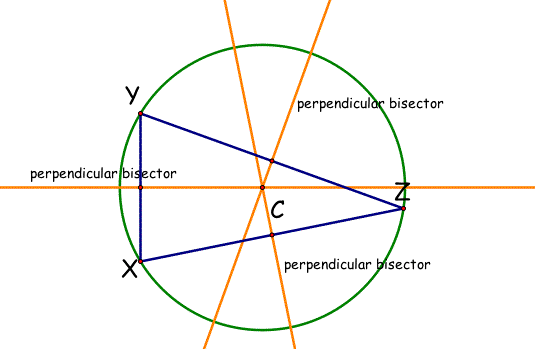
Note: The Circumcenter of a triangle is the center of the circumscribed circle of that triangle. Click on the triangle, XYZ, below in order to create your own triangle & circumscribed circle in GSP.
5. Incenter & 6. Incircle Script Tools
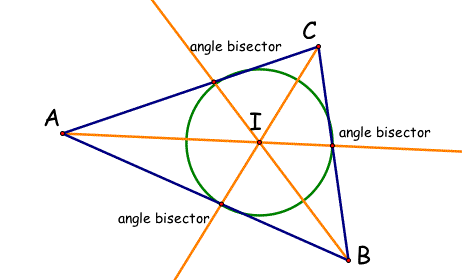
The Incenter of a triangle is the point on the interior of the triangle that is equidistant from the three sides. It can be found by bisecting all three of the angles within a triangle. The point of intersection of the three angle bisectors is called the Incenter. The Incenter is also the center of the inscribed circle of the triangle. See the triangle ABC below showing the 3 angle bisectors in orange and the Incenter, I. Also, the inscribed circle is shown in green.
Click on this triangle to open GSP and use a script tool to create your own Incenter /Incircle triangle.
7. Medial Triangle Script Tool
The Medial Triangle is created by connecting the midpoints of the sides of a triangle. The smaller, shaded triangle in the figure below is the medial triangle of the larger triangle. Click on the triangle below to open GSP and use a script tool to create your own medial triangle.
8. Orthocenter, Mid-segment triangle Script Tool
Click on the triangle figure below to create your own mid segment triangle and its Orthocenter in GSP.
9. Orthic Triangle Script Tool
Click on the example triangle below to open GSP.
10. Pedal Triangle Script Tool
See the example below. The shaded triangle, LMN, is the Pedal triangle for triangle ABC and pedal point P. You may click on this diagram to open GSP and create your own pedal triangle using the script tool provided.
11. Nine point circle and 12. Its center Script Tools
Click on either of the figures below to open GSP and create your own 9-pt circle with center.
13. Trisecting a line segment - Script Tool
 Click on the line to
open GSP for trisection script tool.
Click on the line to
open GSP for trisection script tool.
14. Click here for a GSP script tool to create an equilateral triangle, given a side.
15. Click here for a GSP script tool to create a square, given a side.
16. Click here for a GSP script tool to create an isoceles triangle, given base and altitude.
17. Click here for a GSP script tool to create a triangle and the 4 centers (G - Centroid, H - Orthocenter, C - Circumcenter, and I - Incenter).
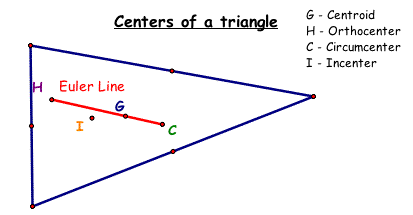
18. Click here for a GSP script tool to find the triangle centers and the Euler Line. See figure below.
19. Click here for a GSP script tool that will draw the locus of a vertex of a fixed angle that subtends a fixed segment.
20. Click here to use a GSP script tool in order to divide a line segment AB into two parts that form the GOLDEN RATIO.
21. Click here for a GSP script tool that creates a PENTAGON given a radius.
22. Click here for a GSP script tool that creates a PENTAGON given a side.
23. Click here for a GSP script tool that will create a HEXAGON given a side.
24. Click here for a GSP script tool that will create an OCTAGON, given a side.