
Explore linear functions with different pairs of f(x) and g(x) for:
h(x) = f(x) + g(x)
h(x) = f(x) * g(x)
h(x) = f(x)/g(x)
h(x) = f(g(x))
First, let f(x) = 2x-3 and g(x) = x + 4
then, h(x) = f(x) + g(x) = 3x + 1.
Now, let h(x) = f(x) * g(x) = 2x^2 + 5x - 12.
Now, let h(x) = f(x)/g(x) = (2x-3)/(x+4) where x can not = -4
Finally, let h(x) = f(g(x)) = 2x +5
Look at the graphs below.


When f(x) = 2x - 3 is graphed we get the linear function below:

When g(x) = x + 4 is graphed we get the linear function below:

When the operation of addition was applied to f(x) and g(x), the result is h(x) = 3x + 1 . When h(x) = 3x +1 is graphed we get another linear function shown below:

When the operation of multiplication is applied to f(x) and g(x), the result is h(x) = 2x^2 + 5x - 12, which is a quadratic funciton. The result is not linear anymore! The graph is a parabola shown below:

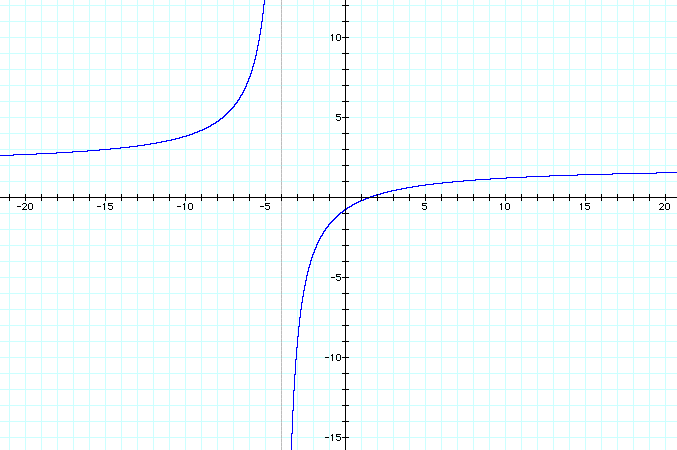
When the operation of division is applied to f(x) and g(x), the result is h(x) = (2x - 3)/(x + 4) where x can not = -4, which is a rational function. The result is not linear or quadratic! The graph has a vertical asymtote at -4 because in mathematics division by zero is not allowed. There is a horizontal asymtote at 2 because as x increases or decreases without bound f(x) approaches 2. See the graph below:

When composition is performed on the two functions f(x) and g(x), the result is h(x) = 2x + 5, which is a linear function! The graph is shown below:

Now, will the same results happen with any two linear functions of the form f(x) = ax + b and g(x) = cx + d?
When addition is performed on f(x) and g(x), the following will result:
f(x) + g(x) = (ax+b) + (cx+d)
combining like terms we have, ax + cx + b + d = (a+c)x +(b+d)
let a+c = e and b+d = f which are constants and h(x) = ex + f which is another linear function!
When multiplication is applied, the following will result:
f(x) * g(x) = (ax +b)(cx + d) = (ac)x^2 + adx + bcx + bd, where ac, ad, and bc are all coefficients of x and bd is a constant. When you combine like terms, h(x) = (ac)x^2 + (ad + bc)x + bd. Replacing the coefficients with one variable we have, ex^2 + fx + g, which is written in quadratic form ax^2 + bx + c. The result is quadratic!
When division is applied, by definition two linear functions divided together is a rational function.
(ax + b)/(cx + d) where (cx + d) can not = 0.
When composition is applied,
h(x) = a(cx +d) + b = acx + ad + b, where ac is a coefficient we will replace with e and ad + b are two constants added together to form some other constant f. Thus,
h(x) = ex + f. Again a linear function!