The following instructions will be followed in this write up:
1. Construct any triangle ABC.
2. Construct the Orthocenter H of triangle ABC.
3. Construct the Orthocenter of triangle HBC.
4. Construct the Orthocenter of triangle HAB.
5. Construct the Orthocenter of triangle HAC.
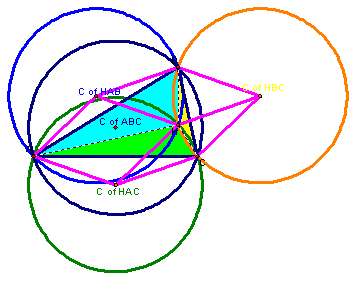
6. Construct the Circumcircles of triangles ABC, HBC, HAB, and HAC.
7. Conjectures?
1.

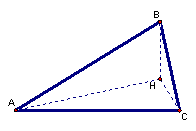
2. The orthocenter is the point of concurrency of the three altitudes of a triangle and is usually denoted by H.
3. The orthocenter of triangle HBC is point A (a vertex of the original triangle).
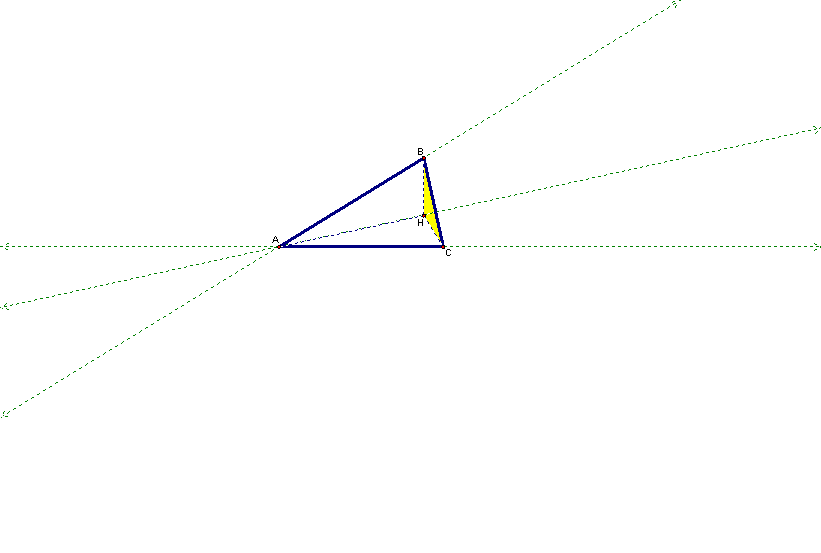
4. The orthocenter of triangle HAB is point C (another vertex of the
original triangle).
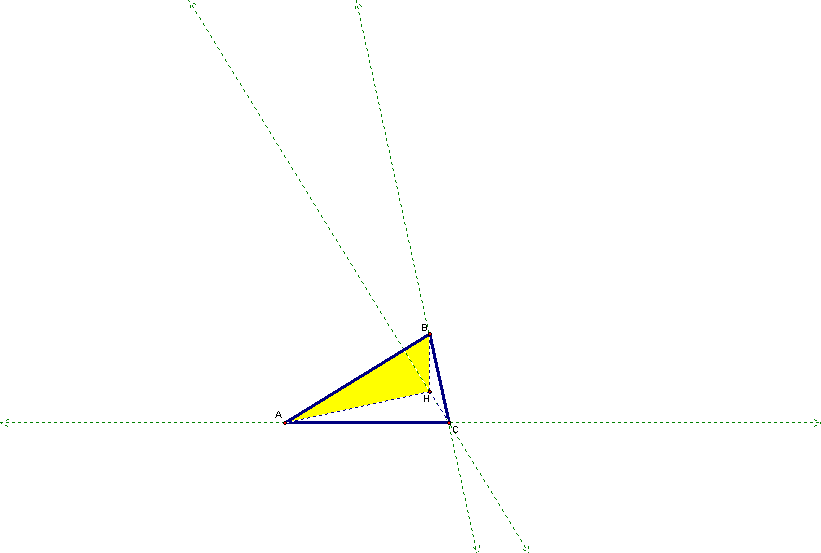
5. The orthocenter of triangle HAC is point B (the other vertex of the original triangle).
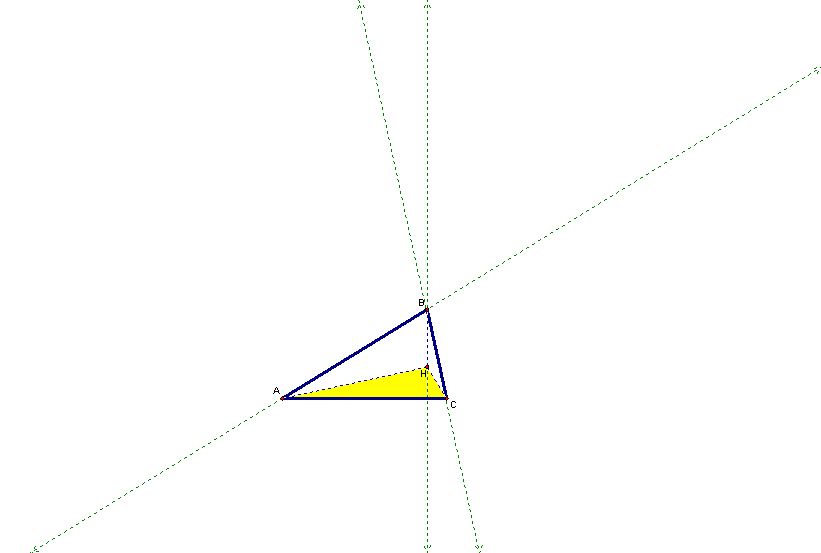
6. The steps involved in constructing a circumcircle are explained in Assignment 4.
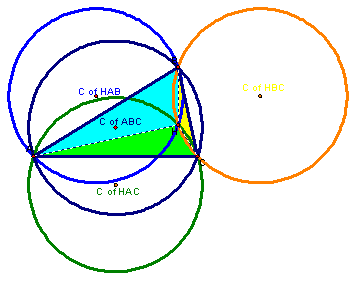
Notice all four circumcircles have the same radius.
7. Click here in order to see a GSP construction. Highlight point B and drag it to H. You should notice triangles AHB and CHB collapse. Triangle AHC becomes larger and B and H switch places. See what happens when you drag the other vertices to H.
An Interesting Thing I Found........
When you connect the centers of the circumcircles with the nearest vertices of the triangles AHB, AHC, or BHC you form a cube!
(Notice the pink line segments.)