Cycloid

In assignment 10, we are exploring the parametric curves.

A parametric curve in the xy-plane is determined by a pair of functions x(t) and y(t). In other words, the curve is given parametrically by the pair of functions x(t) and y(t).

The two equations are usually called the parametric equations of a curve. Parametric equations are a set of equations and each function is expressed by independent variables, which are called parameters. For example, while the equation of a circle in Cartesian coordinates can be given by

,

one set of parametric equations for the circle are given by

x(t) = rcos(t)

y(t) = rsin(t).

 

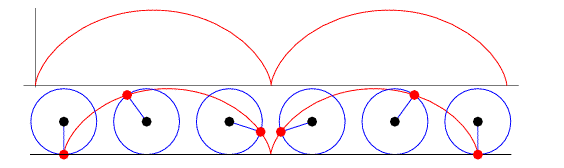
Here I will investigete the cycloid. The cycloid is the locus of a point on the rim of a circle that rolls along a straight line. It was studied and named by Galileo in 1599. First, let's construct the cycloid with GSP and find the parametric equations for the cycloid.

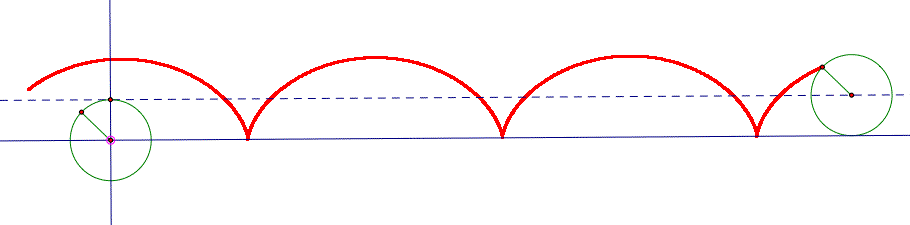
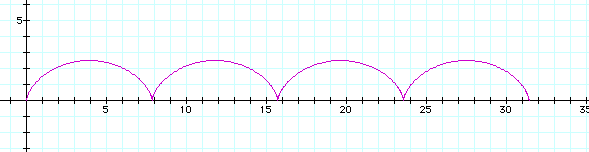
To see animation, open the GSP file(Click here)

and click the animation button.

 

 

If the cycloid has a cusp at the origin and its humps are oriented upward, its parametric equation is

x(t)=a(t-sin(t))

y(t)=a(1-cos(t)).

 

 

Let's take a=1.25 and plot the cycloid. Here I used the Graphing Calculator 3.2.

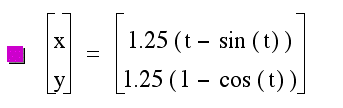
Next let's have more interesting cycloids. How about moving the circle(let's call this blue circle 'wheel') on the circle insteady of the straight line.

Trisect the radius of the big circle and move the wheel around the small circle, whose radius is 2/3 of the radius of the big circle. Here the radius of the wheel is 1/3 of the big circle, so the wheel is moving around the big circle while the center of the wheel is moving around the small circle.

Please click here to see animation.

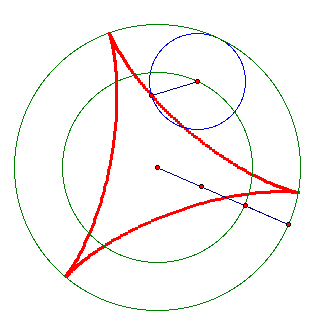
What is going on if we bisect the radius of the big circle?

Let's bisect the radius of the big circle and put the wheel which the radius is 1/2 of the radius of the big circle.

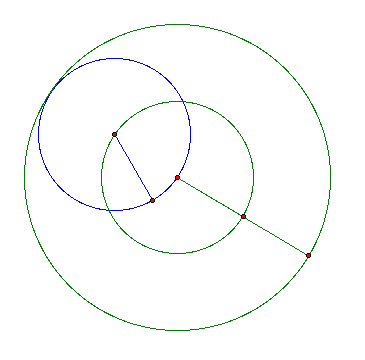
Now, let's play the animation and find the trace.

Here the cycloid is a line, which is a diameter of the big circle. Isn't it interesting?

Please click here to see animaion.

return