Investigation 1.

It has now become a rather standard exercise, with availble technology, to construct graphs to consider the equation

and to overlay several graphs of

for different values of a, b, or c as the other two are held constant.

Let's go over the following basic concepts about the quadratic functions

click here!

How about c?

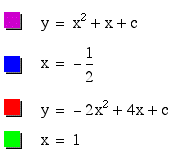
To see the graph movie, click here!

and we can see the information about the coefficient b from below graphs

From these graphs discussion of the patterns for the roots of

can be followed. For example, if we set

for b = -3, -2, -1, 0, 1, 2, 3, and overlay the graphs, the following picture is obtained.

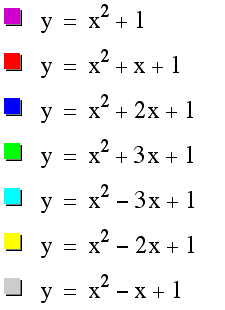
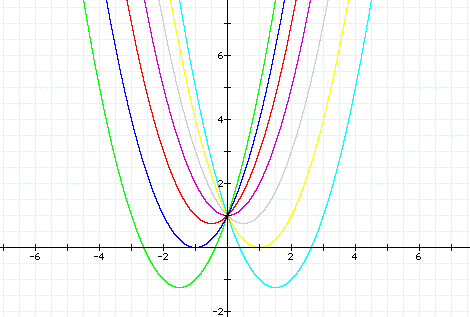
We can discuss the "movement" of a parabola as b is changed. The parabola always passes through the same point on the y-axis ( the point (0,1) with this equation). For b < -2 the parabola will intersect the x-axis in two points with positive x values (i.e. the original equation will have two real roots, both positive). For b = -2, the parabola is tangent to the x-axis and so the original equation has one real and positive root at the point of tangency. For -2 < b < 2, the parabola does not intersect the x-axis -- the original equation has no real roots. Similarly for b = 2 the parabola is tangent to the x-axis (one real negative root) and for b > 2, the parabola intersets the x-axis twice to show two negative real roots for each b.

show that the locus is the parabola

Generalize.

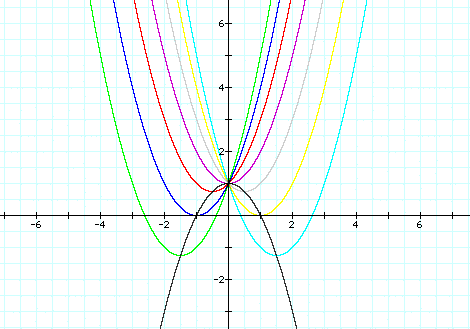
Investigation 2.

Graphs in the xb plane.

Consider again the equation

Now graph this relatio in the xb plane. We get the following graph.

If we take any particular value of b, say b = 3, and overlay this equation on the graph we add a line parallel to the x-axis. If it intersects the curve in the xb plane the intersection points correspond to the roots of the original equation for that value of b. We have the following graph.

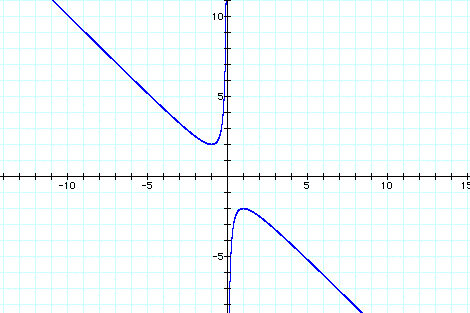
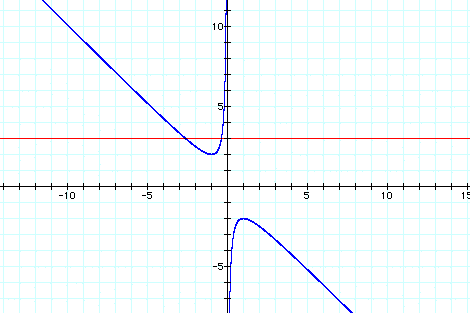
For each value of b we select, we get a horizontal line. It is clear on a single graph that we get two negative real roots of the original equation when b > 2, one negative real root when b = 2, no real roots for -2 < b < 2, One positive real root when b = -2, and two positive real roots when b < -2.

Consider the case when c = - 1 rather than + 1. In that case, it always has roots.

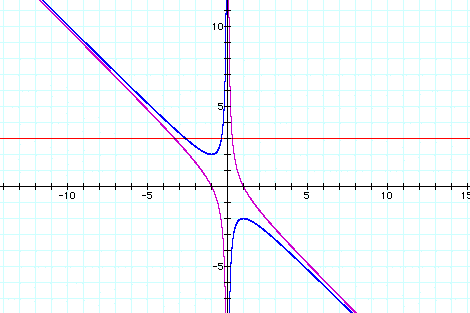
Graph other values of c on the same axex.
we can see it totally by clicking following here !

Investigation 3.

Add the graph of 2x + b = 0 to the picture and discuss its relation to the quadratic formula.

If the sum is

and here is its graph.

and we can know it has always a root from its graph.

Algebraically, it's trivial!

From the quadratic formula, it's the following....

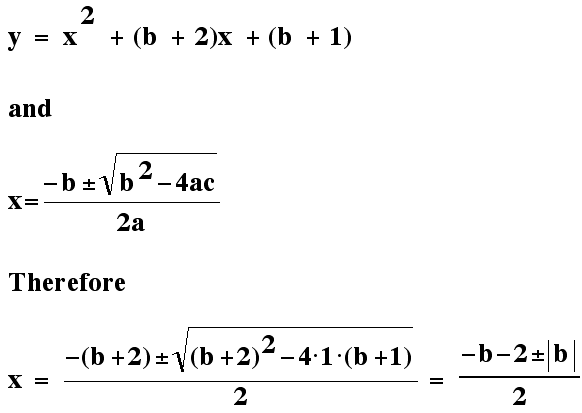
Whatever the real number b is, the equation has at least a root.