

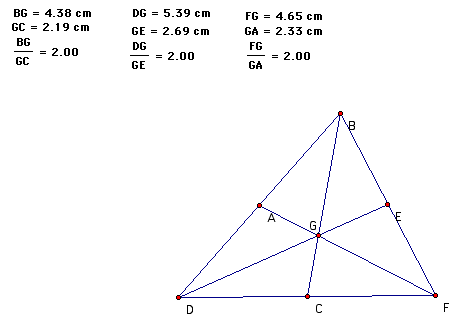
The CENTROID (G) of a triangle is the common intersection of the three medians. A median of a triangle is the segment from a vertex to the midpoint of the opposite side.
By using Geometer's Sketchpad (GSP)
let's Construct the centroid and explore its location for various shapes of triangles.
One more thing, find the property, which is that the centroid divides each median into two segments so that its ratio is 2:1 from vertex regadless of the kind of triangle
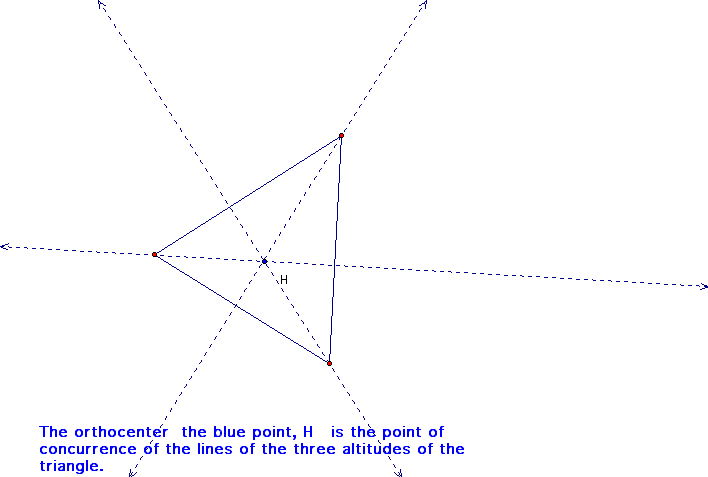
Use GSP to construct an orthocenter H and explore its location for various shapes of triangles. Click the above "orthocenter" in order to make sure that the orthocenter for obtuse triangle is out side of the triangle.
The CIRCUMCENTER (C) of a triangle is the point in the plane equidistant from the three vertices of the triangle. Since a point equidistant from two points lies on the perpendicular bisector of the segment determined by the two points, C is on the perpendicular bisector of each side of the triangle. Note: C may be outside of the triangle.

Construct the circumcenter C and explore its location for various shapes of triangles. It is the center of the CIRCUMCIRCLE (the circumscribed circle) of the triangle.
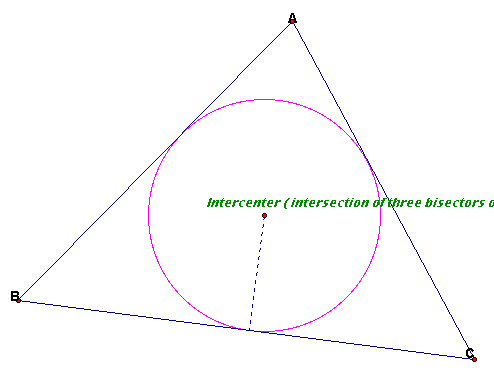
The INCENTER (I) of
a triangle is the point on the interior of the triangle that is
equidistant from the three sides. Since a point interior to an
angle that is equidistant from the two sides of the angle lies
on the angle bisector, then I must be on the angle bisector of
each angle of the triangle.
Use GSP to find a construction of the incenter I and
explore its locationfor various shapes of triangles. The incenter
is the center of the INCIRCLE (the
inscribed circle) of the triangle.
Now, Let's see how different are the position of centers according to different shaped triangles!!
Equilateral Triangle
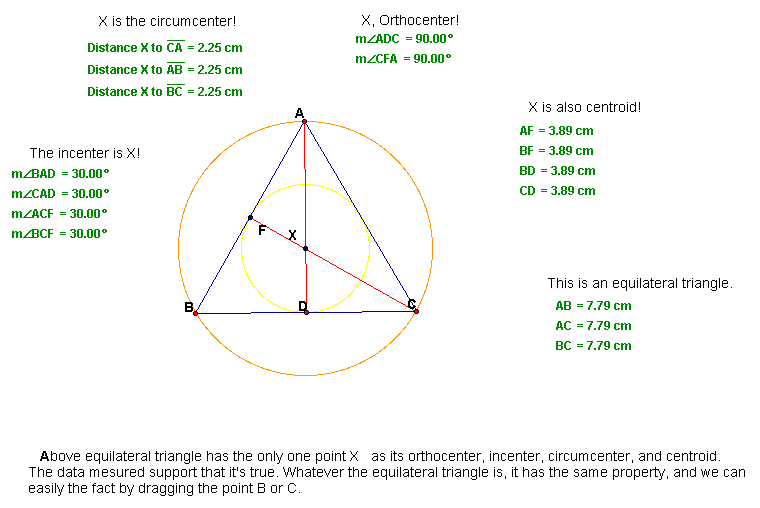
Do you want to see more? Click
Isosceles Triangle
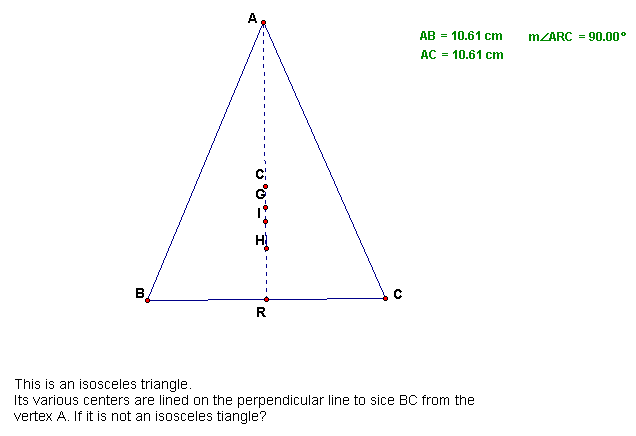
Do you want to see more? Click