

Day 4/Lesson 4: Similar Triangles
Goals:
1. Identify and Understand Similar Triangles
2. Use similar triangles to solve problems.
Technology Opener:
Goal: To Construct similar triangles and to determine a relationship between the corresponding sides of similar triangles.
1. Draw
Triangle ABC.
2. Draw Triangle DEF similar to Triangle ABC.
3. Measure the angles in each triangle.
4. Measure the sides in each triangle.
5. Compare the ratio of the corresponding sides of the triangles.
Now click here to open the instructions in GSP for the construction of similar triangles.
Questions:
1. What did you notice about the angles of the two triangles?
2. What did you notice about the sides of the two triangles?
3. Was there a common relationship between the corresponding sides the triangles?
Investigating Similar Triangles:
Tools: Protractor and straight edge
Activity: Use a protractor and a ruler to draw two noncongruent triangles so that each triangle has a 40 degree angle and a 60 degree angle. Check your drawing by measuring the third angle of each triangle. What is the measurement of the third angle. Why? Measure the lengths of the sides of the triangles and compute the ratios of the lengths of corresponding sides. Are the triangles similar?
When
are triangles similar?
Two triangles are similar when the triangles have the same size angles. In other words all triangles with angle measurments of 40, 60, and 80 degrees are similar no matter what their side lengths are. You have discovered this in the previous two investigations.
Angle- Angle Similarity Postulate:
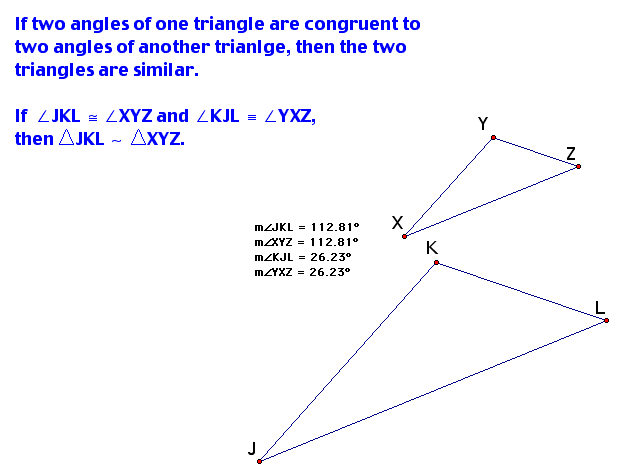
Why does this theorem only talk about two of the angles in the similar triangles?
Think about what we know about the sum of the interior angles of a triangle? In Euclidean Geometry, the sum of the interior angles always addes up to 180 degrees, so if two of the angles of one triangle are congruent to two of the triangles in another triangle, then the third pair of angles must be congruent.
Investigating
Similar Triangles:
Click here to open GSP, follow the instructions and answer the questions about your constructions.
Questions/Exploration:
1. Are the two triangles similar and if so, why?
2. Does it matter where you place point D?
4. Move the points on the large triangle around, does that change the angle measurements or the ratio of the sides, why?
3. What theorem are you using parallel lines and a transversal that cuts the parallel lines?
Click
here to see this construction
complete.
Now we will use the Properties of similar triangles, ratios, and proportions to find angles and lengths of similar triangles:
Example 1:
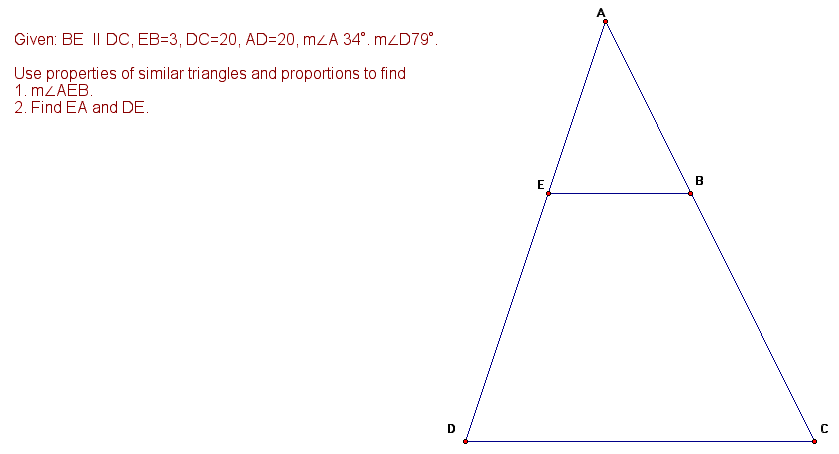
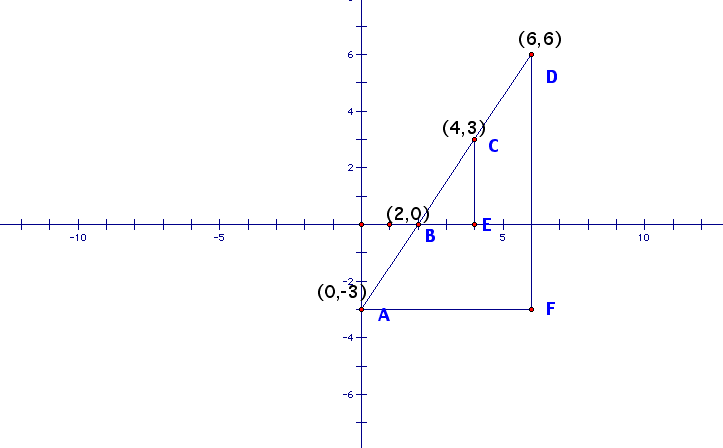
Example 2: Why a Line has only one slope.
Goal: Use the properties of similar triangles to explain why any two points on a line can be used to calculate the slope. Find the slope of the line using both pairs of points shown below.
Solution:
