Assignment
#10
By
Nikki Masson
Parametric
Curves
Assignment
#10
By
Nikki Masson
Parametric
Curves
A parametric
curve in the plane is a pair of functions
x=f(t)
y=g(t)
where
the two continuous functions define ordered pairs (x,y).
Part
I: Get familiar with graphing parametric curves in Graphing Calculator.
Using
graphing calculator, draw x=cos(t) and y=sin(t) from 0<t<pi

Using
graphing calculator, draw x=cos(t) and y=sin(t) from 0<t<2pi

Part
II:
Investigate various values for a and b, when x=cox(at) and
y=sin(bt) for 0<t>2pi
A.
a>b
1.
a=2 and b=1, x=cos(2t) and y=sin(t) for 0<t>2pi
 2.
a=3 and b=1, x=cos(3t) and y=sin(t) for 0<t>2pi
2.
a=3 and b=1, x=cos(3t) and y=sin(t) for 0<t>2pi
 3.
a=4 and b=1, x=cos(4t) and y=sin(t) for 0<t>2pi
3.
a=4 and b=1, x=cos(4t) and y=sin(t) for 0<t>2pi
 4.
a=5 and b=1, x=cos(5t) and y=sin(t) for 0<t>2pi
4.
a=5 and b=1, x=cos(5t) and y=sin(t) for 0<t>2pi
 Observation,
when a is even the grah is not closed and when a is odd, the graph
is closed.
Observation,
when a is even the grah is not closed and when a is odd, the graph
is closed.
B.
a=b:
This is the unit circle from Part I, no matter what the values
of a and b are as long as they are equal.
a=5
and b=5, x=cos(5t) and y=sin(5t) for 0<t>2pi

C.
a<b
1.
a=1 and b=2, x=cos(t) and y=sin(2t) for 0<t>2pi
 2.
a=1 and b=3, x=cos(t) and y=sin(3t) for 0<t>2pi
2.
a=1 and b=3, x=cos(t) and y=sin(3t) for 0<t>2pi
 3.
a=1 and b=4, x=cos(t) and y=sin(4t) for 0<t>2pi
3.
a=1 and b=4, x=cos(t) and y=sin(4t) for 0<t>2pi
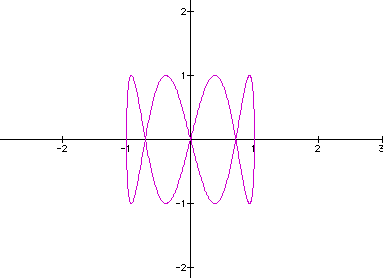 You
can do further investigations into these parametric curves by
changing values for a and b.
You
can do further investigations into these parametric curves by
changing values for a and b.
Part
II:
Investigate various values for a and b, when x=acox(t) and
y=bsin(t) for 0<t>2pi.
A.
a>b
1.
a=2 and b=1, x=2cos(t) and y=sin(t) for 0<t>2pi
 2.
a=3 and b=1, x=3cos(t) and y=sin(t) for 0<t>2pi
2.
a=3 and b=1, x=3cos(t) and y=sin(t) for 0<t>2pi
 We
can see that as we increase a, the ellipse will go from -a to
a.
3.
a=3 and b=2, x=3cos(t) and y=2sin(t) for 0<t>2pi
We
can see that as we increase a, the ellipse will go from -a to
a.
3.
a=3 and b=2, x=3cos(t) and y=2sin(t) for 0<t>2pi
 We
can see from the patterns that the coefficent in front of the
cos(t) and sin(t) tell us the vertices of the ellipse or circle.
We
can see from the patterns that the coefficent in front of the
cos(t) and sin(t) tell us the vertices of the ellipse or circle.
B.
a=b:
x=acox(t) and y=bsin(t) for 0<t>2pi
From our
patterns we have seen in Part III: when a=b, we will have a circle
with the vertices at x=y=a.
1.
a=2 and b=2, x=2cos(t) and y=2sin(t) for 0<t>2pi

C.
a<b
1.
a=1 and b=2, x=cos(t) and y=2sin(t) for 0<t>2pi
 1.
a=2 and b=3, x=2cos(t) and y=3sin(t) for 0<t>2pi
1.
a=2 and b=3, x=2cos(t) and y=3sin(t) for 0<t>2pi
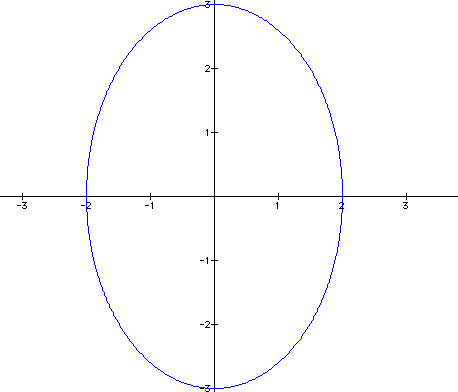 Just
as we suspected, we have ellipse with the vertices at y=3 and
x=2.
Just
as we suspected, we have ellipse with the vertices at y=3 and
x=2.
Return