

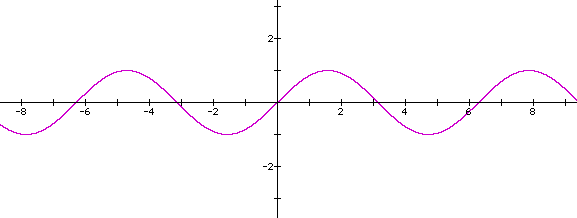
Information about function y=sin(x):
Range and Domain:
The range of the function are the values in the y-direction that the equation hits, which would be the interval [-1,1]. The domain is the set of all real numbers.
Amplitude:
In simple terms the amplitude is the height of the curve. To calculate the amplitude of the curve, it is half of the distance between the maximum and minimum values. For y=sin(x), the maximum value is 1 and the minimum value is -1, so the amplitude of the above curve is 1.
The Period:
The period of the sin curve is how many radians it takes to complete one cycle, or the lengh of one cycle. For y=sin(x), the period is from x=0 to x=2pi.
Part 1: Exploring different values of a
Let us compare our original graph of y=sin(x) to y=a sin(x) for different positive values of a, holding b and c constant at b=c=0.
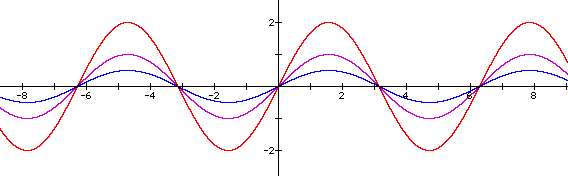
By comparing the red and blue curves to the purple, we observe that as a increases the height is increasing and as a decreases the height is decreasing. This means that a is changing the amplitude of the curve. And by our previous definition of amplitude, this means that the maximum and minimum values are also changing. As the value of a increases to 2 the maximum and minimum values also increase to [-2,2], and as a decreases to (1/2), the maximum and minimum values decrease to [-(1/2),(1/2)].
Now let us look at negative values of a and see how -a affects the curve.
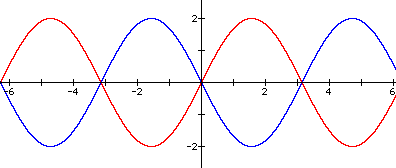
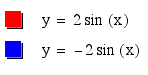
As we can see from the above graph, the negative value of a reflects the curve over the x-axis.
Part 2: Exploring different values of b
Next we will examine how b affects our curve. Let us compare our original graph of y=sin(x) to
y=sin(bx) for different positive values of b, holding a and c constant at a=1 and c=0.
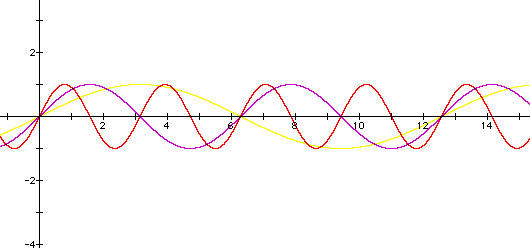
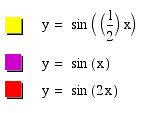
Well, it looks like b is affecting the period of the curve. Recall the period is the number of radians it takes to complete one cycle, or the length it takes to complete one cycle. For y=sin(x) (purple curve) the period is 2pi, but as b increases to 2 (red curve), then the period of y=sin(2x) becomes 4pi. For increasing values of b, the curve is stretched. A smaller number for b has the opposite affect on the curve, it shrinks the curve or makes the period smaller. For y=sin((1/2)x), the period is pi.
Part 3: Exploring different values of c
Lastly, we will compare our original graph of y=sin(x) to y=sin(x+c) for different positive values of c, holding a and b constant at a=b=1.
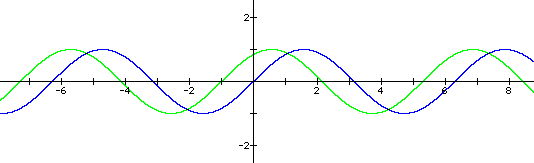
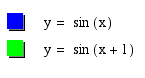
From our observations, the value of c is shifting the curve to the left by 1. So it looks like the coefficient c shifts the curve to the left or right. Now, let us look at a negative value of c.
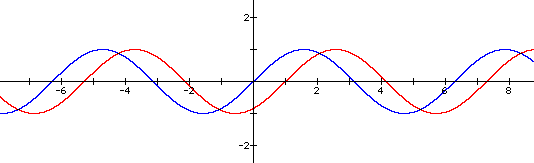
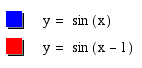
When c is negative, the curve is shifted to the right by the amount of c. In the above graph the red curve is shifted to the right by 1.
Conclusions from exploring y=a sin(bx+c):
The coefficient a changes the height or amplitude of the curve and negative coefficients of a reflect the curve over the x-axis.
The coefficient b changes the period of the curve.
The coefficient c shifts the curve to the right for negative values of c and shifts the curve to the left for positive values of c.