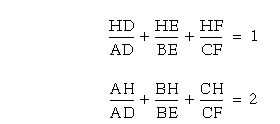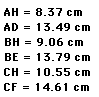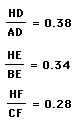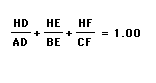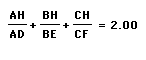Investigation Eight

Altitudes and Orthocenters

Chip Meyer

In this investigation, I will look at how ratios from the orthocenter of a triangle to its points and the feet of the perpendiculars add up to an interesting number. I need to begin by creating a triangle ABC

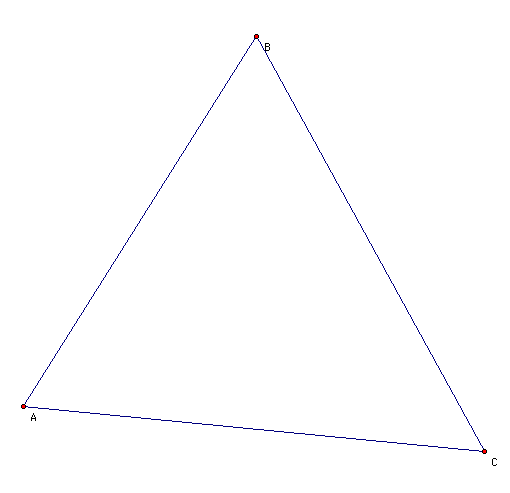
To find the orthocenter of this triangle, I must now find the midpoints of each leg of the triangle.

These midpoints, labeled E, F, and D, now provide me a means to find the orthocenter as I create perpendiculars from each of these midpoints. The intersection created by these perpendiculars will be the orthocenter of my triangle, labeled H.

The ratios I am trying to discover are shown below. Can these numbers be found?

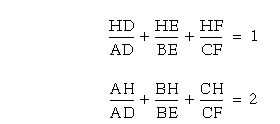
Using the measurement function of the software, I discovered the following about each segment.

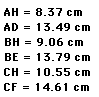
By using these measurements and creating the ratios I was interested in, I found the following.

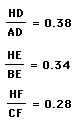
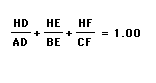
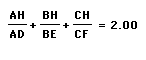
In both cases, the numbers I was trying to find were as I susupected. However, this these ratios due not work for all triangles. In the case of an obtuse triangle where the orthocenter is outside the triangle this does not create the ratios needed to find the proper answers.