
Investigation Seven
Tangent Circles
Chip Meyer
Creating tangent circles poses an interesting question to
students. Do they understand what is really involved in creating
a circle that is tangent to two other circles? The initial steps
seem easy, but the understanding of these steps that may give
them some fits.
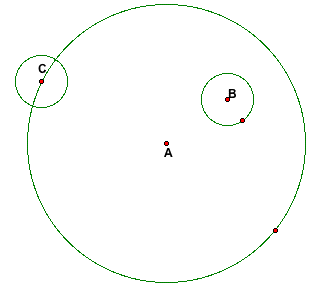
Let's begin with two circles, one with Center B placed inside
the other with Center A. I want to create a circle that is tangent
to Point C on my larger circle as well as tangent to any point
on my smaller circle.

I must now create a circle of the same radius as my Circle
B at Point C.
Now I need to have a line that travels from the Center A of
my large circle through my new circle at Point C and determine
the intersection of these two items. I will label this point as
E.
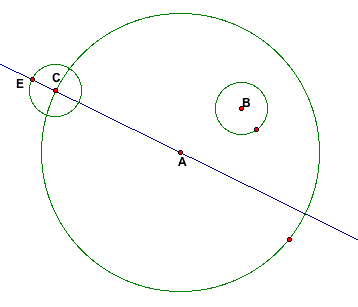
Point E is very important in this investigation because without
it, the true center of the tangent circle can not be found. Using
Point E, I must now create a line segement that travels from Point
E to Point B, the center of my original smaller circle.
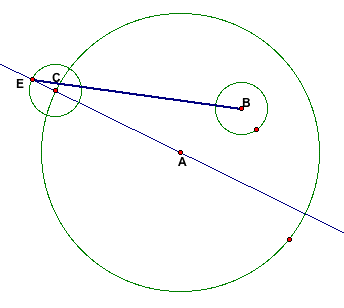
I must now find the midpoint of the segment BE. After this
midpoint is found, a perpendicular line must be created that will
also pass through the segment AE. The intersection of the segment
AE and the perpendicular line from BE, marked X, will provide
the center of the tangent circle I am trying to create.
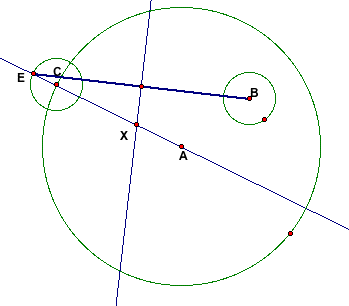
Now, if create a circle with radius XC, I will have a new
circle that is tangent to the inside of Circle A and the outside
of Circle B.
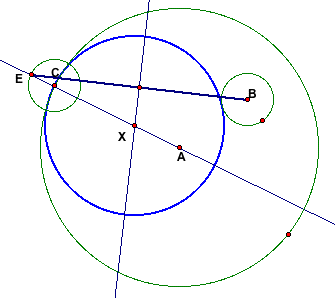
As seen above, I was able to create the circle I originally
intended but not without some trials and tribulations. It is important
for students to think about the importance of segment BE in this
construction. Without it and its perpendicular, one would not
be able to create the tangent circle. Another insteresting part
of this construction is the isosoles triangle EXB that is created
as well. This triangle, shown below in red, is generated in part
due to the midpoint of EB and its perpendicular to segment AE.
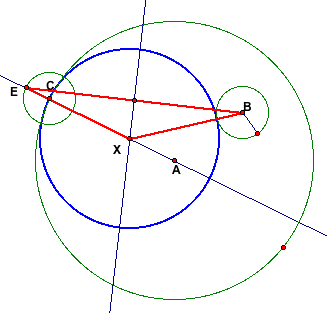
Overall this is a very interesting investigation that high
school geometry students might find useful in their studies.








