
Assignment 10
Parametric Curves
Charles Meyer
Parametric curves are an interesting investigation in to mathematics.
This investigation will look at the affects of different values
of variables on a parametric equation with sine and cosine. The
parametric equation I will look at in this investigation is shown
below
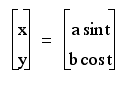
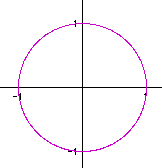
To begin my investigation, I will set my variables a
& b to the value of 1. My t will consist of
a range from 0 to 2Pi. The initial investigation gives the graph
of a circle with a radius of 1.
I now need to take the investigation a bit further and see
how change the value of the a and/or b variable
changes the shape and size of the figure. I begin by changing
the variable a while keeping by variable b as a
constant.
a = 2, b = 1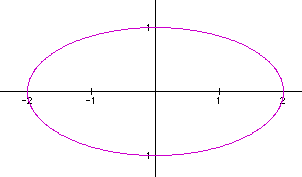
 a
= 3, b = 1
a
= 3, b = 1
As expected, changes with the a variable changes the
curve along the x-axis. I will now verify if the same thing
would occur on the y-axis if I changed the b variable.
b = 2, a = 1 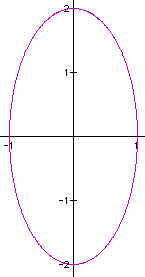
 b
= 3, a = 1
b
= 3, a = 1
Once again, the curves change along the y-axis when
the b variable is change.
But what do the values of a & b really mean
in terms of our circles/ovals? Well, through the investigation
we see that the values assigned to a & b are
actually the intercept of the x & y axis respectfully
as the value of t moves along its range. Further investigation
shows the larger the difference between the two variables the
leaner, more narrow the oval becomes. Two examples are shown below.
a = 0.25, b = 3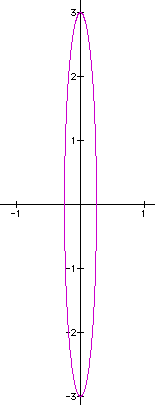
 a = 3, b = 0.25
a = 3, b = 0.25


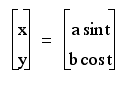


 a
= 3, b = 1
a
= 3, b = 1
 b
= 3, a = 1
b
= 3, a = 1
 a = 3, b = 0.25
a = 3, b = 0.25