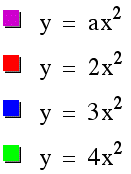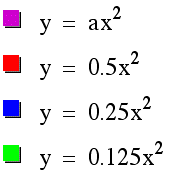Assignment Two
Charles Meyer
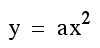
I have decided to investigate a very common
equation as part of assignment two. I chose this equation due
to its frequent use in middle school algebra classes. While most
young people soon realize that the graph of this equation produces
a parabola, it is not easily seen what happens as the value of
a changes.
I will begin by looking at a graph of the
equation with a=1.
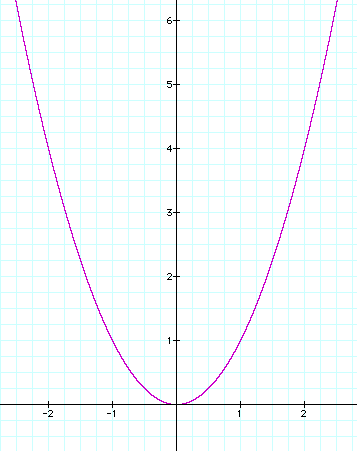
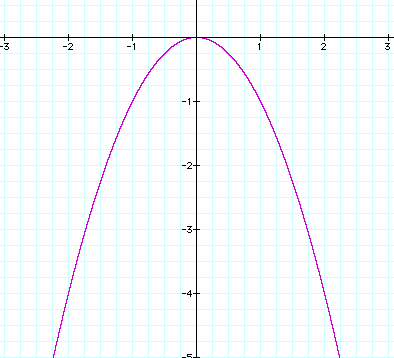
This equation of course produces a parabola
in the positive direction. A negative coeffiecent produces just
the opposite.
The question though to middle schoolers should
be, what happens when the value of a is changed? We can
investigate this through the use of the graphing calculator software
which provides us a way to overlay a series of equations on the
same set of axis and helps demonstrate the changes that are occuring.
I will start by taking values of a and increasing them
by 1.
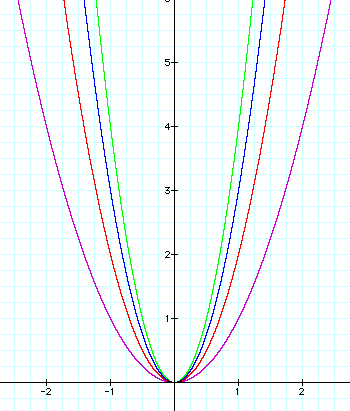
It should be seen that as the value of the
coeffecient increased, the parabola "closed up". In
other words, the distance between the positive and negative y
values became less and less at corresponding x values.
At very large coeffecient values, the parabola would almost seem
to touch the y axis and give the illusion of a single vertical
line. Of course the values of our coeffecient a can become very
small as well.
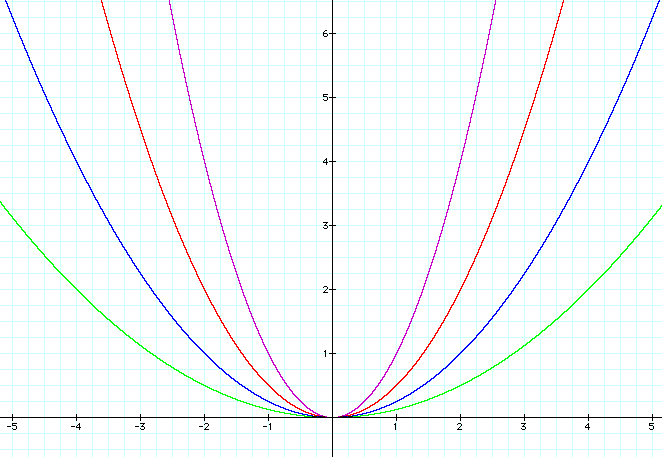
Once again we can see the changes that are
occuring in our graph. As the values of a become smaller,
the parabola "opens up" and spreads out away from the
y-axis. If a were assigned a very small number,
the graph would begin to resemble a horizontal line along the
x-axis.
Middle school and freshmen algebra students
should take note the power of the coefficeint. A change in the
coeffeicent can and will greatly change the look and function
of the equation.