
Investigation Nine
Pedal Triangles
Charles Meyer
In this investigation I will look at the pedal triangle. Along
the way I hope to educate the reader on its orgins as well as
its different properties.
A pedal triangle is formed from the perpendiculars of a given
triangle to a point P in the plane, then the intersection of triangle
ABC to the perpendiculars will form a triangle.
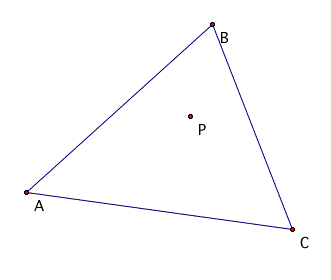
Let's begin with the triangle ABC and Point B.
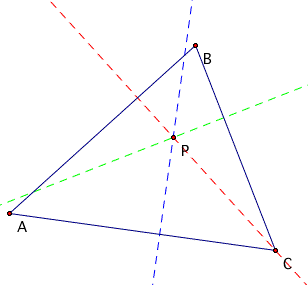
Now we must create the perpendiculars from each segment of
ABC to point P.
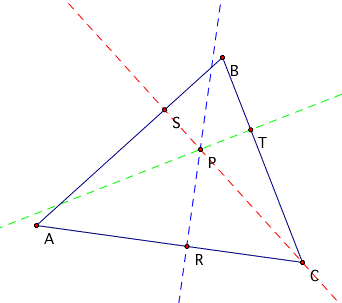
The intersections of the segments and the perpendiculars are
now found and labeled TSR so that the triangle TSR is the pedal
triangle of point P.
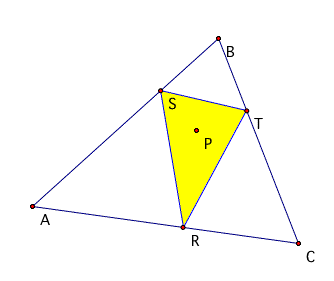
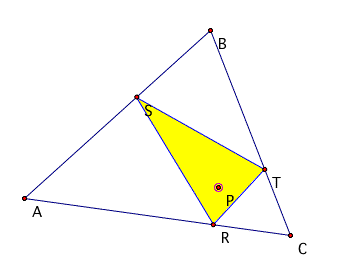
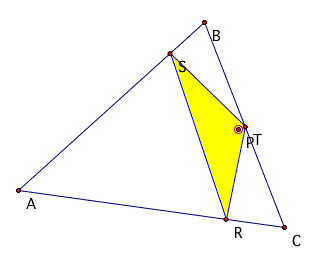
Below are example of the the point P being within different
parts of the triangle. There is not much overall difference to
the triangle at the different points other than size of interior
angles.
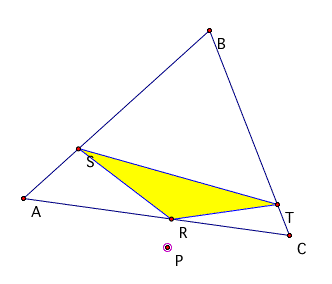
What is really fascinating is the fact that the point P can
also lie outside the triangle as shown below and still a triangle
can be found.
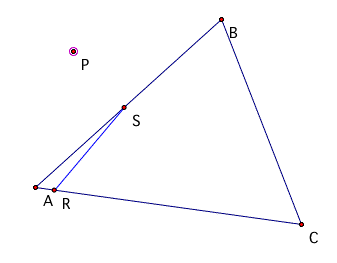
However at some point the triangle is lost as the perpendicular
intersections are unable to form a triangle.
The study of pedal triangles may be helpful to high school
geometry students who are trying to find interesting parts of
triangle construction.









