Centers of a Triangle:

Medial Triangle

By Brooke Norman

For this assignment, I am going to construct a triangle. Using this triangle, I am going to create its Medial triangle.

I began by using the GSP program to construct a triangle. I labeled the 3 points A, B, and C. Take notice to the different colors of the line segments, AB, BC, and CA.

Then, I constructed the midpoints of the 3 sides of triangle ABC. D is the midpoint of AB, E is the midpoint of BC, and F is the midpoint of CA. I then connected the points to make a triangle. This is referred to as the MEDIAL triangle. The Medial triangle is 1/4 of the area of the original triangle, ABC. The lengths of the sides in the medial triangle are 1/2 of the length of their corresponding side in the original triangle, ABC.

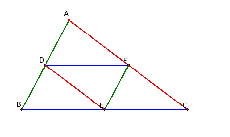
Now that the Medial triangle is constructed, lets see if it fits the definition of a medial triangle. Is the area really 1/4 of the original triangle? Are the length of the sides really 1/2 of that of the original triangle?

I first found the heights of each triangle. For triangle ABC, I took the perpendicular line to point A and line segment BC. For triangle EFD, I took the perpendicular line to point E and line segment FD. I then found the heights by measuring the lengths of AG and HE. I also found the lengths of all of the sides of both the original triangle, ABC; and the Medial triangle, EFD.

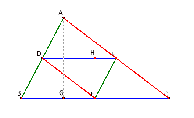
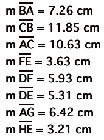
Remember the formula for the area of a triangle is A=¹/₂ Base * Height.

I will now calculate the area of triangle ABC.

A_(ABC)= ¹/₂ (CB)(AG)= ¹/₂ (11.85)(6.42)=38.0385 cm²

A_(EFD)= ¹/₂ (DF)(HE)= ¹/₂ (5.93)(3.21)=9.51765 cm²

Is A_(EFD = ¹/₄ A_(ABC) ?

38.0385/4= 9.509625

Are they the same? Pretty close, they both equal 9.51 cm²

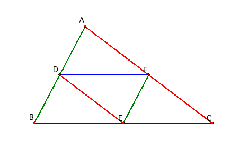
Lastly, I am going to compare the side lengths of the original triangle, ABC; to that of the medial triangle, EFD. In order to help you see the corresponding sides, I labeled them the same colors.

Compare DE & AC. Is 5.31= ¹/₂ 10.63? YES!!

Compare DF & CB. Is 5.93= ¹/₂ 11.85? YES!!

Compare FE & BA. Is 3.63= ¹/₂ 7.26? YES!!

I can say that triangle EFD is indeed the Medial triangle of triangle ABC. I found that all of the sides of the medial triangle are equal to 1¹/₂ of the lengths of the sides of the original triangle, ABC. I also found that the area of the Medial triangle, EFD is ¹/₄ the area of the original triangle, ABC.

Return to Brooke's EMAT 6680 Homepage