Fibonacci’s Sequence

A Natural Occurrence

by

Brooke Norman

What is the Fibonacci sequence?

Fibonacci is a nickname for Leonardo Pisano. He is the man who discovered the pattern of adding two previous numbers together will result in the next number of the pattern, starting at 0 and then 1. The general formula for this sequence is f_n+1 = f_n + f_n-1, f₁ = f₂ =1. The resulting sequence looks like the following. 1, 1, 2, 3, 5, 13, 21, 34, 55, 89, 144, …

Here is an example of the first 25 numbers:

(this was done on Microsoft Excel)

0	0
1	1
2	1
3	2
4	3
5	5
6	8
7	13
8	21
9	34
10	55
11	89
12	144
13	233
14	377
15	610
16	987
17	1597
18	2584
19	4181
20	6765
21	10946
22	17711
23	28657
24	46368

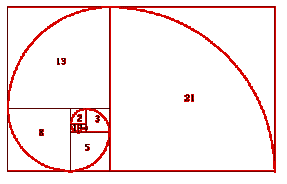
Another part of the Fibonacci sequence is the spiral that it makes. This is made by using the golden ratio. To better see the relationship the sequence has in a more geometrical way, we can look at it as squares. If we start with a square of sides 1, we add another square of sides 1. The result is two. This is the new square with sides 2. If the squares of sides 1 and 2 are added, we get the square of sides 3. This is continued for adding the square of sides 2 and the square of sides 3 to get a square of sides 5. This continues on and we continue to get a spiral.

Here is an example.

What many people don’t know is that this sequence is found in nature. It occurs quite often and is sometimes referred to as a "law of nature."

Click the following links to see different examples in nature.

· Flowers

· Pinecones and Sunflowers

· Honeycombs

Fibonacci would illustrate his sequence by asking people to solve his “Rabbit Problem.”

How many pairs of rabbits will be produced in a year, beginning with a single pair, if in every month each pair bears a new pair which becomes productive from the second month on?

Go ahead. Try it out!

Return to Brooke’s EMAT 6690 homepage